VMS Software / Documentation / VAX RTL Mathematics (MTH$) Manual

VAX RTL Mathematics (MTH$) Manual

Operating System and Version:: OpenVMS VAX Version 7.3

Preface

1. About VSI

VMS Software, Inc. (VSI) is an independent software company licensed by Hewlett Packard Enterprise to develop and support the OpenVMS operating system.

2. Intended Audience

This manual is intended for system and application programmers who write programs that call MTH$ Run-Time Library routines.

3. Document Structure

This manual contains two tutorial chapters, two reference sections, and two appendixes:

Chapter 1, OpenVMS Run-Time Library Mathematics (MTH$) Facility is an introductory chapter that provides guidelines on using the MTH$ scalar routines.
Chapter 2, Vector Routines in MTH$ provides guidelines on using the MTH$ vector routines.
The Chapter 3, Scalar MTH$ Reference Section provides detailed reference information on each scalar mathematics routine contained in the MTH$ facility of the Run-Time Library.
The Chapter 4, Vector MTH$ Reference Section provides detailed reference information on the BLAS Level 1 (Basic Linear Algebra Subroutines) and FOLR (First Order Linear Recurrence) routines.

Reference information is presented using the documentation format described in the VSI OpenVMS Programming Concepts Manual Volume I and Volume II.

. Routine descriptions are in alphabetical order by routine name.

Appendix A, Additional MTH$ Routines lists supported MTH$ routines not included with the routines in the Chapter 3, Scalar MTH$ Reference Section, because they are rarely used.
Appendix B, Vector MTH$ Routine Entry Points contains a table of the vector MTH$ routines that you can call from VAX MACRO.

4. Related Documents

The Run-Time Library routines are documented in a series of reference manuals. A description of how the Run-Time Library routines are accessed and of how OpenVMS features and functionality are available through calls to the MTH$ Run-Time Library appears in VSI OpenVMS Programming Concepts Manual Volume I and Volume II.

Descriptions of the other RTL facilities and their corresponding routines are presented in the following books:

VSI Portable Mathematics Library
OpenVMS RTL DECtalk (DTK$) Manual
VSI OpenVMS RTL Library (LIB$) Manual
VSI OpenVMS RTL General Purpose (OTS$) Manual
OpenVMS RTL Parallel Processing (PPL$) Manual
OpenVMS RTL Screen Management (SMG$) Manual
OpenVMS RTL String Manipulation (STR$) Manual

Application programmers using any language can refer to the Guide to Creating OpenVMS Modular Procedures for writing modular and reentrant code.

High-level language programmers will find additional information on calling Run-Time Library routines in their language reference manuals. Additional information may also be found in the language user’s guide provided with your OpenVMS language software.

5. OpenVMS Documentation

The full VSI OpenVMS documentation set can be found on the VMS Software Documentation webpage at https://docs.vmssoftware.com.

6. VSI Encourages Your Comments

You may send comments or suggestions regarding this manual or any VSI document by sending electronic mail to the following Internet address: <docinfo@vmssoftware.com>. Users who have VSI OpenVMS support contracts through VSI can contact <support@vmssoftware.com> for help with this product.

7. Conventions

The following conventions may be used in this manual:

Convention	Meaning
Ctrl/x	A sequence such as Ctrl/x indicates that you must hold down the key labeled Ctrl while you press another key or a pointing device button.
PF1 x	A sequence such as PF1 x indicates that you must first press and release the key labeled PF1 and then press and release another key or a pointing device button.
...	A horizontal ellipsis in examples indicates one of the following possibilities: Additional optional arguments in a statement have been omitted. The preceding item or items can be repeated one or more times. Additional parameters, values, or other information can be entered.
. . .	A vertical ellipsis indicates the omission of items from a code example or command format; the items are omitted because they are not important to the topic being discussed.
( )	In command format descriptions, parentheses indicate that you must enclose the options in parentheses if you choose more than one.
[ ]	In command format descriptions, brackets indicate optional choices. You can choose one or more items or no items. Do not type the brackets on the command line. However, you must include the brackets in the syntax for VSI OpenVMS directory specifications and for a substring specification in an assignment statement.
[ \| ]	In command format descriptions, vertical bars separate choices within brackets or braces. Within brackets, the choices are options; within braces, at least one choice is required. Do not type the vertical bars on the command line.
{ }	In command format descriptions, braces indicate required choices; you must choose at least one of the items listed. Do not type the braces on the command line.
bold text	This typeface represents the introduction of a new term. It also represents the name of an argument, an attribute, or a reason.
italic text	Italic text indicates important information, complete titles of manuals, or variables. Variables include information that varies in system output (Internal error number), in command lines (/PRODUCER= name), and in command parameters in text (where dd represents the predefined code for the device type).
UPPERCASE TEXT	Uppercase text indicates a command, the name of a routine, the name of a file, or the abbreviation for a system privilege.
`Monospace type`	Monospace type indicates code examples and interactive screen displays. In the C programming language, monospace type in text identifies the following elements: keywords, the names of independently compiled external functions and files, syntax summaries, and references to variables or identifiers introduced in an example.
-	A hyphen at the end of a command format description, command line, or code line indicates that the command or statement continues on the following line.
numbers	All numbers in text are assumed to be decimal unless otherwise noted. Nondecimal radixes—binary, octal, or hexadecimal—are explicitly indicated.

Chapter 1. OpenVMS Run-Time Library Mathematics (MTH$) Facility

The OpenVMS Run-Time Library Mathematics (MTH$) facility contains routines to perform a wide variety of computations including the following:

Floating-point trigonometric function evaluation
Exponentiation
Complex function evaluation
Complex exponentiation
Miscellaneous function evaluation
Vector operations (VAX only)

The OTS$ facility provides additional language-independent arithmetic support routines (see the OpenVMS RTL General Purpose (OTS$) Manual).

This chapter contains an introduction to the MTH$ facility and includes examples of how to call mathematics routines from BASIC, COBOL, Fortran, MACRO, Pascal, PL/I, and Ada.

Chapter 2, Vector Routines in MTH$ contains an overview of the vector routines available on VAX processors.

The Chapter 3, Scalar MTH$ Reference Section describes the MTH$ scalar routines. The Chapter 4, Vector MTH$ Reference Section describes the MTH$ vector routines.

1.1. Entry Point Names

The names of the mathematics routines are formed by adding the MTH$ prefix to the function names.

When function arguments and returned values are of the same data type, the first letter of the name indicates this data type. When function arguments and returned values are of different data types, the first letter indicates the data type of the returned value, and the second letter indicates the data type of the arguments.

The letters used as data type prefixes are listed below.

Letter	Data Type
I	Word
J	Longword
D	D_floating
G	G_floating
H	H_floating
C	F_floating complex
CD	D_floating complex
CG	G_floating complex

Generally, F-floating data types have no letter designation. For example, MTH$SIN returns an F-floating value of the sine of an F-floating argument and MTH$DSIN returns a D-floating value of the sine of a D-floating argument. However, in some of the miscellaneous functions, F-floating data types are referenced by the letter designation A.

1.2. Calling Conventions

For calling conventions specific to the MTH$ vector routines, refer to Chapter 2, Vector Routines in MTH$.

All calls to mathematics routines, as described in the Format section of each routine, accept arguments passed by reference. JSB entry points accept arguments passed by value.

All mathematics routines return values in R0 or R0/R1 except those routines for which the values cannot fit in 64 bits. D-floating complex, G-floating complex, and H-floating values are data structures which are larger than 64 bits. Routines returning values that cannot fit in registers R0/R1 return their function values into the first argument in the argument list.

The notation JSB MTH$NAME_Rn, where n is the highest register number referenced, indicates that an equivalent JSB entry point is available. Registers R0:Rn are not preserved.

Routines with JSB entry points accept a single argument in R0:Rm, where m , which is defined in the following table, is dependent on the data type.

Data Type	m
F_floating	0
D_floating	1
G_floating	2
H_floating	3

A routine returning one value returns it to registers R0:Rm.

When a routine returns two values (for example, MTH$SINCOS), the first value is returned in R0:Rm and the second value is returned in (R<m+1>:R<2*m+1>).

Note that for routines returning a single value, n>=m. For routines returning two values, n>=2*m + 1.

In general, CALL entry points for mathematics routines do the following:

Disable floating-point underflow
Enable integer overflow
Cause no floating-point overflow or other arithmetic traps or faults
Preserve all other enabled operations across the CALL

JSB entry points execute in the context of the caller with the enable operations as set by the caller. Since the routines do not cause arithmetic traps or faults, their operation is not affected by the setting of the arithmetic trap enables, except as noted.

For more detailed information on CALL and JSB entry points, refer to the VSI OpenVMS Programming Concepts Manual Volume I and Volume II.

1.3. Algorithms

For those mathematics routines having corresponding algorithms, the complete algorithm can be found in the Description section of the routine description appearing in the Scalar MTH$ Reference Section of this manual.

1.4. Condition Handling

Error conditions are indicated by using the VAX signaling mechanism. The VAX signaling mechanism signals all conditions in mathematics routines as SEVERE by calling LIB$SIGNAL. When a SEVERE error is signaled, the default handler causes the image to exit after printing an error message. A user-established condition handler can be written to cause execution to continue at the point of the error by returning SS$_CONTINUE. A mathematics routine returns to its caller after the contents of R0/R1 have been restored from the mechanism argument vector CHF$L_MCH_SAVR0/R1. Thus, the user-established handler should correct CHF$L_MCH_SAVR0/R1 to the desired function value to be returned to the caller of the mathematics routine.

D-floating complex, G-floating complex, and H-floating values cannot be corrected with a user-established condition handler, because R2/R3 is not available in the mechanism argument vector.

Note that it is more reliable to correct R0 and R1 to resemble R0 and R1 of a double-precision floating-point value. A double-precision floating-point value correction works for both single- and double-precision values.

If the correction is not performed, the floating-point reserved operand –0.0 is returned. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Accessing the floating-point reserved operand will cause a reserved operand fault. See the OpenVMS RTL Library (LIB$) Manual for a complete description of how to write user condition handlers for SEVERE errors.

A few mathematics routines signal floating underflow if the calling program (JSB or CALL) has enabled floating underflow faults or traps.

All mathematics routines access input arguments and the real and imaginary parts of complex numbers using floating-point instructions. Therefore, a reserved operand fault can occur in any mathematics routine.

1.5. Complex Numbers

A complex number y is defined as an ordered pair of real numbers r and i, where r is the real part and i is the imaginary part of the complex number.

y=(r,i)

OpenVMS supports three floating-point complex types: F-floating complex,

D-floating complex, and G-floating complex. There is no H-floating complex data type.

Run-Time Library mathematics routines that use complex arguments require a pointer to a structure containing two x-floating values to be passed by reference for each argument. The first x-floating value contains r, the real part of the complex number. The second x-floating value contains i, the imaginary part of the complex number. Similarly, Run-Time Library mathematics routines that return complex function values return two x-floating values. Some Language Independent Support (OTS$) routines also calculate complex functions.

Note that complex functions have no JSB entry points.

1.6. Mathematics Routines Not Documented in the MTH$ Reference Section

The mathematics routines in Table 1.1, “Additional Mathematics Routines” are not found in the reference section of this manual. Instead, their entry points and argument information are listed in Appendix A, Additional MTH$ Routines.

A reserved operand fault can occur for any floating-point input argument in any mathematics routine. Other condition values signaled by each mathematics routine are indicated in the footnotes.

Table 1.1. Additional Mathematics Routines

Entry Point	Function
Absolute Value Routines
MTH$ABS	F-floating absolute value
MTH$DABS	D-floating absolute value
MTH$GABS	G-floating absolute value
MTH$HABS	H-floating absolute value?
MTH$IIABS	Word absolute value?
MTH$JIABS	Longword absolute value?
Bitwise AND Operator Routines
MTH$IIAND	Bitwise AND of two word parameters
MTH$JIAND	Bitwise AND of two longword parameters
F-Floating Conversion Routines
MTH$DBLE	Convert F-floating to D-floating (exact)
MTH$GDBLE	Convert F-floating to G-floating (exact)
MTH$IIFIX	Convert F-floating to word (truncated)?
MTH$JIFIX	Convert F-floating to longword (truncated)?
Floating-Point Positive Difference Routines
MTH$DIM	Positive difference of two F-floating parameters?
MTH$DDIM	Positive difference of two D-floating parameters?
MTH$GDIM	Positive difference of two G-floating parameters?
MTH$HDIM	Positive difference of two H-floating parameters?^,?
MTH$IIDIM	Positive difference of two word parameters?
MTH$JIDIM	Positive difference of two longword parameters?
Bitwise Exclusive OR Operator Routines
MTH$IIEOR	Bitwise exclusive OR of two word parameters
MTH$JIEOR	Bitwise exclusive OR of two longword parameters
Integer to Floating-Point Conversion Routines
MTH$FLOATI	Convert word to F-floating (exact)
MTH$DFLOTI	Convert word to D-floating (exact)
MTH$GFLOTI	Convert word to G-floating (exact)
MTH$FLOATJ	Convert longword to F-floating (rounded)
MTH$DFLOTJ	Convert longword to D-floating (exact)
MTH$GFLOTJ	Convert longword to G-floating (exact)
Conversion to Greatest Floating-Point Integer Routines
MTH$FLOOR	Convert F-floating to greatest F-floating integer
MTH$DFLOOR	Convert D-floating to greatest D-floating integer
MTH$GFLOOR	Convert G-floating to greatest G-floating integer
MTH$HFLOOR	Convert H-floating to greatest H-floating integer?
Floating-Point Truncation Routines
MTH$AINT	Convert F-floating to truncated F-floating
MTH$IINT	Convert F-floating to truncated word?
MTH$JINT	Convert F-floating to truncated longword?
MTH$DINT	Convert D-floating to truncated D-floating
MTH$IIDINT	Convert D-floating to truncated word?
MTH$JIDINT	Convert D-floating to truncated longword?
MTH$GINT	Convert G-floating to truncated G-floating
MTH$IIGINT	Convert G-floating to truncated word?
MTH$JIGINT	Convert G-floating to truncated longword?
MTH$HINT	Convert H-floating to truncated H-floating?
MTH$IIHINT	Convert H-floating to truncated word?
MTH$JIHINT	Convert H-floating to truncated longword?
Bitwise Inclusive OR Operator Routines
MTH$IIOR	Bitwise inclusive OR of two word parameters
MTH$JIOR	Bitwise inclusive OR of two longword parameters
Maximum Value Routines
MTH$AIMAX0	F-floating maximum of n word parameters
MTH$AJMAX0	F-floating maximum of n longword parameters
MTH$IMAX0	Word maximum of n word parameters
MTH$JMAX0	Longword maximum of n longword parameters
MTH$AMAX1	F-floating maximum of n F-floating parameters
MTH$DMAX1	D-floating maximum of n D-floating parameters
MTH$GMAX1	G-floating maximum of n G-floating parameters
MTH$HMAX1	H-floating maximum of n H-floating parameters?
MTH$IMAX1	Word maximum of n F-floating parameters?
MTH$JMAX1	Longword maximum of n F-floating parameters?
Minimum Value Routines
MTH$AIMIN0	F-floating minimum of n word parameters
MTH$AJMIN0	F-floating minimum of n longword parameters
MTH$IMIN0	Word minimum of n word parameters
MTH$JMIN0	Longword minimum of n longword parameters
MTH$AMIN1	F-floating minimum of n F-floating parameters
MTH$DMIN1	D-floating minimum of n D-floating parameters
MTH$GMIN1	G-floating minimum of n G-floating parameters
MTH$HMIN1	H-floating minimum of n H-floating parameters?
MTH$IMIN1	Word minimum of n F-floating parameters?
MTH$JMIN1	Longword minimum of n F-floating parameters?
Remainder Routines
MTH$AMOD	Remainder of two F-floating parameters, arg1/arg2?^,?
MTH$DMOD	Remainder of two D-floating parameters, arg1/arg2?^,?
MTH$GMOD	Remainder of two G-floating parameters, arg1/arg2?
MTH$HMOD	Remainder of two H-floating parameters, arg1/arg2?^,?
MTH$IMOD	Remainder of two word parameters, arg1/arg2?
MTH$JMOD	Remainder of two longword parameters, arg1/arg2?
Floating-Point Conversion to Nearest Value Routines
MTH$ANINT	Convert F-floating to nearest F-floating integer
MTH$ININT	Convert F-floating to nearest word integer?
MTH$JNINT	Convert F-floating to nearest longword integer?
MTH$DNINT	Convert D-floating to nearest D-floating integer
MTH$IIDNNT	Convert D-floating to nearest word integer?
MTH$JIDNNT	Convert D-floating to nearest longword integer?
MTH$GNINT	Convert G-floating to nearest G-floating integer
MTH$IIGNNT	Convert G-floating to nearest word integer?
MTH$JIGNNT	Convert G-floating to nearest longword integer?
MTH$HNINT	Convert H-floating to nearest H-floating integer?
MTH$IIHNNT	Convert H-floating to nearest word integer?
MTH$JIHNNT	Convert H-floating to nearest longword integer?
Bitwise Complement Operator Routines
MTH$INOT	Bitwise complement of word parameter
MTH$JNOT	Bitwise complement of longword parameter
Floating-Point Multiplication Routines
MTH$DPROD	D-floating product of two F-floating parameters?
MTH$GPROD	G-floating product of two F-floating parameters
Bitwise Shift Operator Routines
MTH$IISHFT	Bitwise shift of word
MTH$JISHFT	Bitwise shift of longword
Floating-Point Sign Function Routines
MTH$SGN	F- or D-floating sign function
MTH$SIGN	F-floating transfer of sign of y to sign of x
MTH$DSIGN	D-floating transfer of sign of y to sign of x
MTH$GSIGN	G-floating transfer of sign of y to sign of x
MTH$HSIGN	H-floating transfer of sign of y to sign of x?
MTH$IISIGN	Word transfer of sign of y to sign of x
MTH$JISIGN	Longword transfer of sign of y to sign of x
Conversion of Double to Single Floating-Point Routines
MTH$SNGL	Convert D-floating to F-floating (rounded)?
MTH$SNGLG	Convert G-floating to F-floating (rounded)?^,?

1.7. Examples of Calls to Run-Time Library Mathematics Routines

1.7.1. BASIC Example

The following BASIC program uses the H-floating data type. BASIC also supports the D-floating, F-floating, and G-floating data types, but does not support the complex data types.

10     !+
       ! Sample program to demonstrate a call to MTH$HEXP from BASIC.
       !-

       EXTERNAL SUB MTH$HEXP ( HFLOAT, HFLOAT )

       DECLARE HFLOAT X,Y      ! X and Y are H-floating
       DIGITS$ = ’###.#################################’
       X = ’1.2345678901234567891234567892’H
       CALL MTH$HEXP (Y,X)
       A$ = ’MTH$HEXP of ’ + DIGITS$ + ’ is ’ + DIGITS$
       PRINT USING A$, X, Y
       END

The output from this program is as follows:

MTH$HEXP of 1.234567890123456789123456789200000
is 3.436893084346008004973301321342110

1.7.2. COBOL Example

The following COBOL program uses the F-floating and D-floating data types. COBOL does not support the G-floating and H-floating data types or the complex data types.

This COBOL program calls MTH$EXP and MTH$DEXP.

IDENTIFICATION DIVISION.
PROGRAM-ID.    FLOATING_POINT.

Calls MTH$EXP using a Floating Point data type. 
Calls MTH$DEXP using a Double Floating Point data type.

ENVIRONMENT DIVISION.
DATA DIVISION.
WORKING-STORAGE SECTION.
01 FLOAT_PT     COMP-1.
01 ANSWER_F     COMP-1.
01 DOUBLE_PT    COMP-2.
01 ANSWER_D     COMP-2.
PROCEDURE DIVISION.
P0.
        MOVE 12.34 TO FLOAT_PT.
        MOVE 3.456 TO DOUBLE_PT. 

        CALL "MTH$EXP" USING BY REFERENCE FLOAT_PT GIVING ANSWER_F.
        DISPLAY " MTH$EXP of ", FLOAT_PT CONVERSION, " is ", 
                                               ANSWER_F CONVERSION. 

        CALL "MTH$DEXP" USING BY REFERENCE DOUBLE_PT GIVING ANSWER_D.
        DISPLAY " MTH$DEXP of ", DOUBLE_PT CONVERSION, " is ", 
                                               ANSWER_D CONVERSION. 
        STOP RUN.

The output from this example program is as follows:

MTH$EXP of 1.234000E+01 is 2.286620E+05
MTH$DEXP of 3.456000000000000E+00 is
3.168996280537917E+01

1.7.3. Fortran Examples

The first Fortran program below uses the G-floating data type. The second Fortran program below uses the H-floating data type. The third Fortran program below uses the F-floating complex data type. Fortran supports the four floating data types and the three complex data types.

C+
C This Fortran program computes the log base 2 of x, log2(x) in
C G-floating double precision by using the RTL routine MTH$GLOG2.
C
C Declare X and Y and MTH$GLOG2 as double precision values.
C
C MTH$GLOG2 will return a double precision value to variable Y.
C-
 REAL*8 X, Y, MTH$GLOG2 
 X = 16.0
 Y = MTH$GLOG2(X)
 WRITE (6,1) X, Y
1 FORMAT (’ MTH$GLOG2(’,F4.1,’) is ’,F4.1)
END

The output generated by the preceding program is as follows:

MTH$GLOG2(16.0) is 4.0

C+
C This Fortran program computes the log base 2 of x, log2(x) in
C H-floating precision by using the RTL routine MTH$HLOG2.
C
C Declare X and Y and MTH$GLOG2 as REAL*16 values.
C
C MTH$HLOG2 will return a REAL*16 value to variable Y.
C-
 REAL*16 X, Y 
 X = 16.12345678901234567890123456789
 CALL MTH$HLOG2(Y, X)
 WRITE (6,1) X, Y
1 FORMAT (’ MTH$HLOG2(’,F30.27,’) is ’,F30.28)
END

The output generated by the preceding program is as follows:

MTH$HLOG2(16.123456789012345678901234568) is 4.0110891785623860194931388310

C+
C    This Fortran example raises a complex base to
C    a NONNEGATIVE integer power using OTS$POWCJ.
C
C    Declare Z1, Z2, Z3, and OTS$POWCJ as complex values.
C    Then OTS$POWCJ returns the complex result of
C    Z1**Z2:   Z3 = OTS$POWCJ(Z1,Z2),
C    where Z1 and Z2 are passed by value.
C-
        COMPLEX Z1,Z3,OTS$POWCJ
        INTEGER Z2
C+
C    Generate a complex base.
C- 
        Z1 = (2.0,3.0) 
C+
C    Generate an integer power.
C-
        Z2=2  
C+ 
C    Compute the complex value of Z1**Z2.
C- 
        Z3 = OTS$POWCJ( %VAL(REAL(Z1)), %VAL(AIMAG(Z1)), %VAL(Z2))
        TYPE 1,Z1,Z2,Z3 
  1     FORMAT(’ The value of (’,F10.8,’,’,F11.8,’)**’,I1,’ is 
     +  (’,F11.8,’,’,F12.8,’).’)
        END

The output generated by the preceding Fortran program is as follows:

The value of (2.00000000, 3.00000000)**2 is
(-5.00000000, 12.00000000).

1.7.4. MACRO Examples

MACRO and BLISS support JSB entry points as well as CALLS and CALLG entry points. Both MACRO and BLISS support the four floating data types and the three complex data types.

The following MACRO programs show the use of the CALLS and CALLG instructions, as well as JSB entry points.

        .TITLE EXAMPLE_JSB
;+ 
;  This example calls MTH$DEXP by using a MACRO JSB command. 
;  The JSB command expects R0/R1 to contain the quadword input value X. 
;  The result of the JSB will be located in R0/R1. 
;- 
        .EXTRN MTH$DEXP_R6      ;MTH$DEXP is an external routine. 
        .PSECT DATA, PIC, EXE, NOWRT 
X:      .DOUBLE 2.0             ; X is 2.0 
        .ENTRY EXAMPLE_JSB, ^M<> 
        MOVQ   X, R0            ; X is in registers R0 and R1 
        JSB    G^MTH$DEXP_R6    ; The result is returned in R0/R1.
        RET 
        .END   EXAMPLE_JSB

This MACRO program generates the following output:

R0 <-- 732541EC
R1 <-- ED6EC6A6 
That is, MTH$DEXP(2) is 7.3890560989306502

        .TITLE EXAMPLE_CALLG 
;+ 
;  This example calls MTH$HEXP by using a MACRO CALLG command. 
;  The CALLG command expects that the address of the return value 
;  Y, the address of the input value X, and the argument count 2 be 
;  stored in memory; this program stores this information in ARGUMENTS. 
;  The result of the CALLG will be located in R0/R1. 
;- 
        .EXTRN  MTH$HEXP        ; MTH$HEXP is an external routine. 
        .PSECT DATA, PIC, EXE, WRT
ARGUMENTS: 
        .LONG 2                 ; The CALLG will use two arguments. 
        .ADDRESS Y, X           ; The first argument must be the address 
                                ; receiving the computed value, while 
                                ; the second argument is used to 
                                ; compute exp(X). 
X:      .H_FLOATING 2           ; X = 2.0 
Y:      .H_FLOATING 0           ; Y is the result, initially set to 0. 
        .ENTRY  EXAMPLE_G, ^M<> 
        CALLG   ARGUMENTS, G^MTH$HEXP ; CALLG returns the value to Y.
        RET 
        .END    EXAMPLE_G

The output generated by this MACRO program is as follows:

address of Y  <-- D8E64003 
              <-- 4DDA4B8D 
              <-- 3A3BDCC3 
              <-- B68BA206 
That is, MTH$HEXP of 2.0 returns
7.38905609893065022723042746057501

        .TITLE EXAMPLE_CALLS 
;+ 
;  This example calls MTH$HEXP by using the MACRO CALLS command. 
;  The CALLS command expects the SP to contain the H-floating address of 
;  the return value, the address of the input argument X, and the argument 
;  count 2. The result of the CALLS will be located in registers R0-R3. 
;- 
      .EXTRN MTH$HEXP        ; MTH$HEXP is an external routine. 
      .PSECT DATA, PIC, EXE, WRT 
Y:    .H_FLOATING 0          ; Y is the result, initially set to 0.
X:    .H_FLOATING 2          ; X = 2 
      .ENTRY  EXAMPLE_S, ^M<> 
      MOVAL   X, -(SP)       ; The address of X is in the SP.
      MOVAL   Y, -(SP)       ; The address of Y is in the SP 
      CALLS   Y, G^MTH$HEXP  ; The value is returned to the address of Y.
      RET 
      .END    EXAMPLE_S

The output generated by this program is as follows:

address of Y  <-- D8E64003 
              <-- 4DDA4B8D 
              <-- 3A3BDCC3 
              <-- B68BA206 
That is, MTH$HEXP of 2.0 returns
7.38905609893065022723042746057501

        .TITLE COMPLEX_EX1 
;+ 
;  This example calls MTH$CLOG by using a MACRO CALLG command. 
;  To compute the complex natural logarithm of Z = (2.0,1.0) register 
;  R0 is loaded with 2.0, the real part of Z, and register R1 is loaded 
;  with 1.0, the imaginary part of Z. The CALLG to MTH$CLOG 
;  returns the value of the natural logarithm of Z in 
;  registers R0 and R1. R0 gets the real part of Z and R1 
;  gets the imaginary part. 
;- 
       .EXTRN  MTH$CLOG 
       .PSECT  DATA, PIC, EXE, NOWRT 
ARGS:  .LONG   1               ; The CALLG will use one argument. 
       .ADDRESS REAL           ; The one argument that the CALLG 
                               ; uses is the address of the argument 
                               ; of MTH$CLOG. 
REAL:  .FLOAT  2               ; real part of Z is 2.0 
IMAG:  .FLOAT  1               ; imaginary part Z is 1.0 
       .ENTRY  COMPLEX_EX1, ^M<> 
       CALLG   ARGS, G^MTH$CLOG; MTH$CLOG returns the real part of the 
                               ; complex natural logarithm in R0 and 
                               ; the imaginary part in R1. 
       RET 
       .END    COMPLEX_EX1

This program generates the following output:

R0 <--- 0210404E
R1 <--- 63383FED 
That is, MTH$CLOG(2.0,1.0) is
(0.8047190,0.4636476)

        .TITLE COMPLEX_EX2 
;+ 
;  This example calls MTH$CLOG by using a MACRO CALLS command. 
;  To compute the complex natural logarithm of Z = (2.0,1.0) register 
;  R0 is loaded with 2.0, the real part of Z, and register R1 is loaded 
;  with 1.0, the imaginary part of Z. The CALLS to MTH$CLOG 
;  returns the value of the natural logarithm of Z in registers R0 
;  and R1. R0 gets the real part of Z and R1 gets the imaginary 
;  part. 
;- 
       .EXTRN  MTH$CLOG 
       .PSECT  DATA, PIC, EXE, NOWRT 
REAL:  .FLOAT  2               ; real part of Z is 2.0 
IMAG:  .FLOAT  1               ; imaginary part Z is 1.0 
       .ENTRY  COMPLEX_EX2, ^M<> 
       MOVAL   REAL, -(SP)     ; SP <-- address of Z. Real part of Z is 
                               ; in @(SP) and imaginary part is in
       CALLS   #1, G^MTH$CLOG  ; @(SP)+4. 
                               ; MTH$CLOG return the real part of the 
                               ; complex natural logarithm in R0 and 
                               ; the imaginary part in R1. 
       RET 
       .END    COMPLEX_EX2

This MACRO example program generates the following output:

R0 <--- 0210404E
R1 <--- 63383FED 
That is, MTH$CLOG(2.0,1.0) is
(0.8047190,0.4636476)

1.7.5. Pascal Examples

The following Pascal programs use the D-floating and H-floating data types. Pascal also supports the F-floating and G-floating data types. Pascal does not support the complex data types.

{+} 
{ Sample program to demonstrate a call to MTH$DEXP from PASCAL. 
{-} 
PROGRAM CALL_MTH$DEXP (OUTPUT); 
{+} 
{ Declare variables used by this program. 
{-} 
VAR 
    X : DOUBLE := 3.456;        { X,Y are D-floating unless overridden }
    Y : DOUBLE;                 { with /DOUBLE qualifier on compilation } 
{+} 
{ Declare the RTL routine used by this program. 
{-} 
[EXTERNAL,ASYNCHRONOUS] 
                  FUNCTION MTH$DEXP (VAR value : DOUBLE) : DOUBLE; EXTERN; 
BEGIN 
    Y := MTH$DEXP (x); 
    WRITELN (’MTH$DEXP of ’, X:5:3, ’ is ’, Y:20:16);
END.

The output generated by this Pascal program is as follows:

MTH$DEXP of 3.456 is 31.6899656462382318

{+} 
{ Sample program to demonstrate a call to MTH$HEXP from PASCAL. 
{-} 
PROGRAM CALL_MTH$HEXP (OUTPUT); 
{+} 
{ Declare variables used by this program. 
{-} 
VAR 
    X : QUADRUPLE := 1.2345678901234567891234567892;  { X is H-floating } 
    Y : QUADRUPLE;                                    { Y is H-floating } 
{+} 
{ Declare the RTL routine used by this program. 
{-} 
[EXTERNAL,ASYNCHRONOUS] PROCEDURE MTH$HEXP (VAR h_exp : QUADRUPLE;
value : QUADRUPLE); EXTERN; 
BEGIN 
    MTH$HEXP (Y,X); 
    WRITELN (’MTH$HEXP of ’, X:30:28, ’ is ’, Y:35:33);
END.

This Pascal program generates the following output:

MTH$DEXP of 3.456 is 31.6899656462382318

1.7.6. PL/I Examples

The following PL/I programs use the D-floating and H-floating data types to test entry points. PL/I also supports the F-floating and G-floating data types. PL/I does not support the complex data types.

/*
*                                                                     *
*     This program tests a MTH$D entry point                          *
*                                                                     *
*/
TEST: PROC OPTIONS (MAIN) ; 
      DCL (MTH$DEXP) 
              ENTRY (FLOAT(53)) RETURNS (FLOAT(53));
      DCL OPERAND FLOAT(53); 
      DCL RESULT FLOAT(53); 
/*** Begin test ***/ 
     OPERAND = 3.456; 
     RESULT = MTH$DEXP(OPERAND); 
     PUT EDIT (’MTH$DEXP of ’, OPERAND, ’ is ’,
         RESULT)(A(12),F(5,3),A(4),F(20,15)); 
END TEST;

The output generated by this PL/I program is as follows:

MTH$DEXP of 3.456 is 31.689962805379165

/* 
*                                                                     *
*     This program tests a MTH$H entry point.                         *
*     Note that in the PL/I statement below, the /G-float switch      *
*     is needed to compile both G- and H-floating point MTH$ routines.*/
TEST: PROC OPTIONS (MAIN) ; 
      DCL (MTH$HEXP) 
              ENTRY (FLOAT (113), FLOAT (113)) ;
      DCL OPERAND FLOAT (113); 
      DCL RESULT FLOAT (113); 
/*** Begin test ***/ 
      OPERAND = 1.234578901234567891234567892;
      CALL MTH$HEXP(RESULT,OPERAND); 
      PUT EDIT (’MTH$HEXP of ’, OPERAND, ’ is ’,
          RESULT) (A(12),F(29,27),A(4),F(29,27)); 
END TEST;

To run this program, use the following DCL commands:

$ PLI/G_FLOAT EXAMPLE 
$ LINK EXAMPLE 
$ RUN EXAMPLE

This program generates the following output:

MTH$HEXP of 1.234578901234567891234567892 is
3.436930928565989790506225633

1.7.7. Ada Example

The following Ada program demonstrates the use of MTH$ routines in a manner that an actual program might use. The program performs the following steps:

Reads a floating-point number from the terminal
Calls MTH$SQRT to obtain the square root of the value read
Calls MTH$JNINT to find the nearest integer of the square root
Displays the result

This example runs on VSI Ada for OpenVMS VAX.

-- This Ada program calls the MTH$SQRT and MTH$JNINT routines. 
-- 
with FLOAT_MATH_LIB; 
    -- Package FLOAT_MATH_LIB is an instantiation of the generic package 
    -- MATH_LIB for the FLOAT datatype. This package provides the most 
    -- common mathematical functions (SQRT, SIN, COS, etc.) in an easy 
    -- to use fashion. An added benefit is that the Compaq Ada compiler 
    -- will use the faster JSB interface for these routines.
with MTH; 
    -- Package MTH defines all the MTH$ routines. It should be used when 
    -- package MATH_LIB is not sufficient. All functions are defined here 
    -- as "valued procedures" for consistency.
with FLOAT_TEXT_IO, INTEGER_TEXT_IO, TEXT_IO; 
procedure ADA_EXAMPLE is
    FLOAT_VAL: FLOAT;
    INT_VAL: INTEGER; 
begin 
    -- Prompt for initial value.
    TEXT_IO.PUT ("Enter value: ");
    FLOAT_TEXT_IO.GET (FLOAT_VAL);
    TEXT_IO.NEW_LINE;
    -- Take the square root by using the SQRT routine from package 
    -- FLOAT_MATH_LIB. The compiler will use the JSB interface 
    -- to MTH$SQRT. 
    FLOAT_VAL := FLOAT_MATH_LIB.SQRT (FLOAT_VAL); 
    -- Find the nearest integer using MTH$JNINT. Argument names are 
    -- the same as those listed for MTH$JNINT in the reference 
    -- section of this manual. 
    MTH.JNINT (F_FLOATING => FLOAT_VAL, RESULT => INT_VAL); 
    -- Write the result.
    TEXT_IO.PUT ("Result is: ");
    INTEGER_TEXT_IO.PUT (INT_VAL);
    TEXT_IO.NEW_LINE; 
end ADA_EXAMPLE;

To run this example program, use the following DCL commands:

$ CREATE/DIR [.ADALIB] 
$ ACS CREATE LIB [.ADALIB] 
$ ACS SET LIB [.ADALIB] 
$ ADA ADA_EXAMPLE 
$ ACS LINK ADA_EXAMPLE 
$ RUN ADA_EXAMPLE

The preceding Ada example generates the following output:

Enter value: 42.0 
Result is:                  6

Chapter 2. Vector Routines in MTH$

This chapter discusses four sets of routines provided by the RTL MTH$ facility that support vector processing. These routines are as follows:

Basic Linear Algebra Subroutines (BLAS) Level 1
First Order Linear Recurrence (FOLR) routines
Vector versions of existing scalar routines
Fast-Vector math routines

2.1. BLAS — Basic Linear Algebra Subroutines Level 1

BLAS Level 1 routines perform vector operations, such as copying one vector to another, swapping vectors, and so on. These routines help you take advantage of vector processing speed. BLAS Level 1 routines form an integral part of many mathematical libraries, such as LINPACK and EISPACK.? Because these routines usually occur in the innermost loops of user code, the Run-Time Library provides versions of the BLAS Level 1 that are tuned to take best advantage of the VAX vector processors.

Two versions of BLAS Level 1 are provided. To use either of these libraries, link in the appropriate shareable image. The libraries are:

Scalar BLAS — contained in the shareable image BLAS1RTL
Vector BLAS (routines that take advantage of vectorization) — contained in the shareable image VBLAS1RTL

Note

To call the scalar BLAS from a program that runs on scalar hardware, specify the routine name preceded by BLAS1$ (for example, BLAS1$xCOPY). To call the vector BLAS from a program that runs on vector hardware, specify the routine name preceded by BLAS1$V (for example, BLAS1$VxCOPY).

This manual describes both the scalar and vector versions of BLAS Level 1, but for simplicity the vector prefix (BLAS1$V) is used exclusively. Remember to remove the letter V from the routine prefix when you want to call the scalar version.

If you are a VSI Fortran programmer, do not specify BLAS vector routines explicitly. Specify the Fortran intrinsic function name only. The VSI Fortran 77 for OpenVMS VAX Systems compiler determines whether the vector or scalar version of a BLAS routine should be used. The Fortran /BLAS=([NO]INLINE,[NO]MAPPED) qualifier controls how the compiler processes calls to BLAS Level 1. If /NOBLAS is specified, then all BLAS calls are treated as ordinary external routines. The default of INLINE means that calls to BLAS Level 1 routines will be treated as known language constructs, and VAX object code will be generated to compute the corresponding operations at the call site, rather than call a user-supplied routine. If the Fortran qualifier /VECTOR or /PARALLEL=AUTO is in effect, the generated code for the loops may use vector instructions or be decomposed to run on multiple processors. If MAPPED is specified, these calls will be treated as calls to the optimized implementations of these routines in the BLAS1$ and BLAS1$V portions of the MTH$ facility. For more information on the Fortran /BLAS qualifier, refer to the DEC Fortran Performance Guide for OpenVMS VAX Systems .

Ten families of routines form BLAS Level 1. (BLAS1$VxCOPY is one family of routines, for example.) These routines operate at the vector-vector operation level. This means that BLAS Level 1 performs operations on one or two vectors. The level of complexity of the computations (in other words, the number of operations being performed in a BLAS Level 1 routine) is of the order n (the length of the vector).

Each family of routines in BLAS Level 1 contains routines coded in single precision, double precision (D and G formats), single precision complex, and double precision complex (D and G formats). BLAS Level 1 can be broadly classified into three groups:

BLAS1$VxCOPY, BLAS1$VxSWAP, BLAS1$VxSCAL and BLAS1$VxAXPY:
These routines return vector outputs for vector inputs. The results of all these routines are independent of the order in which the elements of the vector are processed. The scalar and vector versions of these routines return the same results.
BLAS1$VxDOT, BLAS1$VIxAMAX, BLAS1$VxASUM, and BLAS1$VxNRM2:
These routines are all reduction operations that return a scalar value. The results of these routines (except BLAS1$VIxAMAX) are dependent upon the order in which the elements of the vector are processed. The scalar and vector versions of BLAS1$VxDOT, BLAS1$VxASUM, and BLAS1$VxNRM2 can return different results. The scalar and vector versions of BLAS1$VIxAMAX return the same results.
BLAS1$VxROTG and BLAS1$VxROT: These routines are used for a particular application (plane rotations), unlike the routines in the previous two categories. The results of BLAS1$VxROTG and BLAS1$VxROT are independent of the order in which the elements of the vector are processed. The scalar and vector versions of these routines return the same results.

Table 2.1, “Functions of BLAS Level 1” lists the functions and corresponding routines of BLAS Level 1.

Table 2.1. Functions of BLAS Level 1

Function	Routine	Data Type
Copy a vector to another vector	BLAS1$VSCOPY BLAS1$VDCOPY BLAS1$VCCOPY BLAS1$VZCOPY	Single Double (D-floating or G-floating) Single complex Double complex (D-floating or G-floating)
Swap the elements of two vectors	BLAS1$VSSWAP BLAS1$VDSWAP BLAS1$VCSWAP BLAS1$VZSWAP	Single Double (D-floating or G-floating) Single complex Double complex (D-floating or G-floating)
Scale the elements of a vector	BLAS1$VSSCAL BLAS1$VDSCAL BLAS1$VGSCAL BLAS1$VCSCAL BLAS1$VCSSCAL BLAS1$VZSCAL BLAS1$VWSCAL BLAS1$VZDSCAL BLAS1$VWGSCAL	Single Double (D-floating) Double (G-floating) Single complex with complex scale Single complex with real scale Double complex with complex scale (D-floating) Double complex with complex scale (G-floating) Double complex with real scale (D-floating) Double complex with real scale (G-floating)
Multiply a vector by a scalar and add a vector	BLAS1$VSAXPY BLAS1$VDAXPY BLAS1$VGAXPY BLAS1$VCAXPY BLAS1$VZAXPY BLAS1$VWAXPY	Single Double (D-floating) Double (G-floating) Single complex Double complex (D-floating) Double complex (G-floating)
Obtain the index of the first element of a vector having the largest absolute value	BLAS1$VISAMAX BLAS1$VIDAMAX BLAS1$VIGAMAX BLAS1$VICAMAX BLAS1$VIZAMAX BLAS1$VIWAMAX	Single Double (D-floating) Double (G-floating) Single complex Double complex (D-floating) Double complex (G-floating)
Obtain the sum of the absolute values of the elements of a vector	BLAS1$VSASUM BLAS1$VDASUM BLAS1$VGASUM BLAS1$VSCASUM BLAS1$VDZASUM BLAS1$VGWASUM	Single Double (D-floating) Double (G-floating) Single complex Double complex (D-floating) Double complex (G-floating)
Obtain the inner product of two vectors	BLAS1$VSDOT BLAS1$VDDOT BLAS1$VGDOT BLAS1$VCDOTU BLAS1$VCDOTC BLAS1$VZDOTU BLAS1$VWDOTU BLAS1$VZDOTC BLAS1$VWDOTC	Single Double (D-floating) Double (G-floating) Single complex unconjugated Single complex conjugated Double complex unconjugated (D-floating) Double complex unconjugated (G-floating) Double complex conjugated (D- floating) Double complex conjugated (G- floating)
Obtain the Euclidean norm of the vector	BLAS1$VSNRM2 BLAS1$VDNRM2 BLAS1$VGNRM2 BLAS1$VSCNRM2 BLAS1$VDZNRM2 BLAS1$VGWNRM2	Single Double (D-floating) Double (G-floating) Single complex Double complex (D-floating) Double complex (G-floating)
Generate the elements for a Givens plane rotation	BLAS1$VSROTG BLAS1$VDROTG BLAS1$VGROTG BLAS1$VCROTG BLAS1$VZROTG BLAS1$VWROTG	Single Double (D-floating) Double (G-floating) Single complex Double complex (D-floating) Double complex (G-floating)
Apply a Givens plane rotation	BLAS1$VSROT BLAS1$VDROT BLAS1$VGROT BLAS1$VCSROT BLAS1$VZDROT BLAS1$VWGROT	Single Double (D-floating) Double (G-floating) Single complex Double complex (D-floating) Double complex (G-floating)

For a detailed description of these routines, refer to Chapter 4, Vector MTH$ Reference Section.

2.1.1. Using BLAS Level 1

The following sections provide some guidelines for using BLAS Level 1.

2.1.1.1. Memory Overlap

The vector BLAS produces unpredictable results when any element of the input argument shares a memory location with an element of the output argument. (An exception is a special case found in the BLAS1$VxCOPY routines.)

The vector BLAS and the scalar BLAS can yield different results when the input argument overlaps the output array.

2.1.1.2. Round-Off Effects

For some of the routines in BLAS Level 1, the final result is independent of the order in which the operations are performed. However, in other cases (for example, some of the reduction operations), efficiency dictates that the order of operations on a vector machine be different from the natural order of operations. Because round-off errors are dependent upon the order in which the operations are performed, some of the routines will not return results that are bit-for-bit identical to the results obtained by performing the operations in natural order.

Where performance can be increased by the use of a backup data type, this has been done. This is the case for BLAS1$VSNRM2, BLAS1$VSCNRM2, BLAS1$VSROTG, and BLAS1$VCROTG. The use of a backup data type can also yield a gain in accuracy over the scalar BLAS.

2.1.1.3. Underflow and Overflow

In accordance with LINPACK convention, underflow, when it occurs, is replaced by a zero. A system message informs you of overflow. Because the order of operations for some routines is different from the natural order, overflow might not occur at the same array element in both the scalar and vector versions of the routines.

2.1.1.4. Notational Definitions

The vector BLAS (except the BLAS1$VxROTG routines) perform operations on vectors. These vectors are defined in terms of three quantities:

A vector length, specified as n
An array or a starting element in an array, specified as x
An increment or spacing parameter to indicate the distance in number of array elements to skip between successive vector elements, specified as incx

Suppose x is a real array of dimension ndim , n is its vector length, and incx is the increment used to access the elements of a vector X. The elements of vector X, X_i,i = l, ..., n, are stored in x. If incx is greater than or equal to 0, then X_i is stored in the following location:

x(l + (i - l) * incx)

However, if incx is less than 0, then X_i is stored in the following location:

x(l + (n - i) * |incx|)

It therefore follows that the following condition must be satisfied:

ndim≥l+ (n - l) * |incx|

A positive value for incx is referred to as forward indexing, and a negative value is referred to as backward indexing. A value of zero implies that all of the elements of the vector are at the same location, x₁.

Suppose ndim = 20 and n = 5. In this case, incx = 2 implies that X₁, X₂, X₃, X₄, and X₅ are located in array elements x₁, x₃, x₅, x₇, and x₉.

If, however, incx is negative, then X₁, X₂, X₃, X₄, and X₅ are located in array elements x₉, x₇, x₅, x₃, and x₁. In other words, when incx is negative, the subscript of x decreases as i increases.

For some of the routines in BLAS Level 1, incx = 0 is not permitted. In the cases where a zero value for incx is permitted, it means that x₁ is broadcast into each element of the vector X of length n.

You can operate on vectors that are embedded in other vectors or matrices by choosing a suitable starting point of the vector. For example, if A is an n1 by n2 matrix, column j is referenced with a length of n1 , starting point A (1,j), and increment 1. Similarly, row i is referenced with a length of n2 , starting point A (i,1), and increment n1.

2.2. FOLR — First Order Linear Recurrence Routines

The MTH$ FOLR routines provide a vectorized algorithm for the linear recurrence relation. A linear recurrence uses the result of a previous pass through a loop as an operand for subsequent passes through the loop and prevents the vectorization of a loop.

The only error checking performed by the FOLR routines is for a reserved operand.

There are four families of FOLR routines in the MTH$ facility. Each family accepts each of four data types (longword integer, F-floating, D-floating, and G-floating). However, all of the arrays you specify in a single FOLR call must be of the same data type.

For a detailed description of these routines, see Chapter 4, Vector MTH$ Reference Section.

2.2.1. FOLR Routine Name Format

The four families of FOLR routines are as follows:

MTH$VxFOLRy_MA_V15
MTH$VxFOLRy_z_V8
MTH$VxFOLRLy_MA_V5
MTH$VxFOLRLy_z_V2

where:

x = J for longword integer, F for F-floating, D for D-floating, or G for G-floating

y = P for a positive recursion element, or N for a negative recursion element

z = M for multiplication, or A for addition

The FOLR entry points end with _Vn, where n is an integer between 0 and 15 that denotes the vector registers that the FOLR routine uses. For example, MTH$VxFOLRy_z_V8 uses vector registers V0 through V8.

To determine which group of routines you should use, match the task in the left column in Table 2–2 that you need the routine to perform with the method of storage that you need the routine to employ. The point where these two tasks meet shows the FOLR routine you should call.

Table 2.2. Determining the FOLR Routine You Need

Tasks	Save each iteration in an array	Save only last result in a variable
Multiplication AND addition	MTH$VxFOLRy_MA_V15	MTH$VxFOLRLy_MA_V5
Multiplication OR addition	MTH$VxFOLRy_z_V8	MTH$VxFOLRLy_z_V2

2.2.2. Calling a FOLR Routine

Save the contents of V0 through Vn before calling a FOLR routine if you need it after the call. The variable n can be 2, 5, 8, or 15, depending on the FOLR routine entry point. (The OpenVMS Calling Standard specifies that a called procedure may modify all of the vector registers. The FOLR routines modify only the vector registers V0 through Vn.)

The MTH$ FOLR routines assume that all of the arrays are of the same data type.

2.3. Vector Versions of Existing Scalar Routines

Vector forms of many MTH$ routines are provided to support vectorized compiled applications. Vector versions of key F-floating, D-floating, and G-floating scalar routines employ vector hardware, while maintaining identical results with their scalar counterparts. Many of the scalar algorithms have been redesigned to ensure identical results and good performance for both the vector and scalar versions of each routine. All vectorized routines return bit-for-bit identical results as the scalar versions.

You can call the vector MTH$ routines directly if your program is written in VAX MACRO. If you are a Fortran programmer, specify the Fortran intrinsic function name only. The Fortran compiler will then determine whether the vector or scalar version of a routine should be used.

2.3.1. Exceptions

You should not attempt to recover from an MTH$ vector exception. After an MTH$ vector exception, the vector routines cannot continue execution, and nonexceptional values might not have been computed.

2.3.2. Underflow Detection

In general, if a vector instruction results in the detection of both a floating overflow and a floating underflow, only the overflow will be signaled.

Some scalar routines check to see if a user has enabled underflow detection. For each of those scalar routines, there are two corresponding vector routines: one that always enables underflow checking and one that never enables underflow checking. (In the latter case, underflows produce a result of zero.) The Fortran compiler always chooses the vector version that does not signal underflows, unless the user specifies the /CHECK=UNDERFLOW qualifier. This ensures that the check is performed but does not impair vector performance for those not interested in underflow detection.

2.3.3. Vector Routine Name Format

Use one of the formats in Table 2–3 to call (from VAX MACRO) a vector math routine that enables underflow signaling. (The E in the routine name means enabled underflow signaling.)

Table 2.3. Vector Routine Format — Underflow Signaling Enabled

Format	Type of Routine
MTH$VxSAMPLE _E_Ry_Vz	Real valued math routine
MTH$VCxSAMPLE _E_Ry_Vz	Complex valued math routine
OTS$SAMPLE q_E_Ry_Vz	Power routine or complex multiply and divide

Use one of the formats in Table 2–4 to call (from VAX MACRO) a vector math routine that does not enable underflow signaling.

Table 2.4. Vector Routine Format — Underflow Signaling Disabled

Format	Type of Routine
MTH$VxSAMPLE _Ry_Vz	Real valued math routine
MTH$VCxSAMPLE _Ry_Vz	Complex valued math routine
OTS$SAMPLE q_Ry_Vz	Power routine or complex multiply and divide

In the preceding formats, the following conventions are used:

x

The letter A (or blank) for F-floating, D for D-floating, G for G-floating.

y

A number between 0 and 11 (inclusive). Ry means that the scalar registers R0 through Ry will be used by the routine SAMPLE. You must save these registers.

z

A number between 0 and 15 (inclusive). Vz means that the vector registers V0 through Vz will be used by the routine SAMPLE. You must save these registers.

q

Two letters denoting the base and power data type, as follows:

RR	F-floating base raised to an F-floating power
RJ	F-floating base raised to a longword power
DD	D-floating base raised to a D-floating power
DJ	D-floating base raised to a longword power
GG	G-floating base raised to a G-floating power
GJ	G-floating base raised to a longword power
JJ	Longword base raised to a longword power

2.3.4. Calling a Vector Math Routine

You can call the vector MTH$ routines directly if your program is written in VAX MACRO.

Note

If you are a VSI Fortran programmer, do not specify the MTH$ vector routines explicitly. Specify the Fortran intrinsic function name only. The Fortran compiler determines whether the vector or scalar version of a routine should be used.

In the following examples, keep in mind that vector real arguments are passed in V0, V1, and so on, and vector real results are returned in V0. On the other hand, vector complex arguments are passed in V0 and V1, V2, and V3, and so on. Vector complex results are returned in V0 and V1.

Argument	Argument Passed Register	Results Returned Register
Vector real arguments	V0, V1,...	V0
Vector complex arguments	V0 and V1, V2 and V3,...	V0 and V1

Example 1

The following example shows how to call the vector version of MTH$EXP. Assume that you do not want underflows to be signaled, and you need to use the current contents of all vector and scalar registers after the invocation. Before you can call the vector routine from VAX MACRO, perform the following steps.

Find EXP in the column of scalar names in Appendix B, Vector MTH$ Routine Entry Points to determine:
- The full vector routine name: MTH$VEXP_R3_V6
- How the routine is invoked (CALL or JSB): JSB
- The scalar registers that must be saved: R0 through R3 (as specified by R3 in MTH$VEXP_R3_V6)
- The vector registers that must be saved: V0 through V6 (as specified by V6 in MTH$VEXP_R3_V6)
- The vector registers used to hold the input arguments: V0
- The vector registers used to hold the output arguments: V0
- If there is a vector version that signals underflow (not needed in this example)
Save the scalar registers R0, R1, R2, and R3.
Save the vector registers V0, V1, V2, V3, V4, V5, and V6.
Save the vector mask register VMR.
Save the vector count register VCR.
Load the vector length register VLR.
Load the vector register V0 with the argument for MTH$EXP.
JSB to MTH$VEXP_R3_V6.
Store result in memory.
Restore all scalar and vector registers except for V0. (The results of the call to MTH$VEXP_R3_V6 are stored in V0.)

The following MACRO program fragment shows this example. Assume that:

V0 through V6 and R0 through R3 have been saved.
R4 points to a vector of 60 input values.
R6 points to the location where the results of MTH$VEXP_R3_V6 will be stored.
R5 contains the stride in bytes.

Note that MTH$VEXP_R3_V6 denotes an F-floating data type because there is no letter between V and E in the routine name. (For further explanation, refer to Section 2.3.3, “Vector Routine Name Format”.) The stride (the number of array elements that are skipped) must be a multiple of 4 because each F-floating value requires 4 bytes.

MTVLR   #60                 ; Load VLR
MOVL    #4, R5              ; Stride
VLDL    (R4), R5, V0        ; Load V0 with the actual arguments
JSB     G^MTH$VEXP_R3_V6    ; JSB to MTH$VEXP
VSTL    V0, (R6), R5        ; Store the results

Example 2

The following example demonstrates how to call the vector version of OTS$POWDD with a vector base raised to a scalar power. Before you can call the vector routine from VAX MACRO, perform the following steps.

Find POWDD (V S) in the column of scalar names in Appendix B, Vector MTH$ Routine Entry Points to determine:
- The full vector routine name: OTS$VPOWDD_R1_V8
- How the routine is invoked (CALL or JSB): CALL
- The scalar registers that must be saved: R0 through R1 (as specified by R1 in OTS$VPOWDD_R1_V8)
- The vector registers that must be saved: V0 through V8 (as specified by V8 in OTS$VPOWDD_R1_V8)
- The vector registers used to hold the input arguments: V0, R0
- The vector registers used to hold the output arguments: V0
- If there is a vector version that signals underflow (not needed in this example)
Save the scalar registers R0 and R1.
Save the vector registers V0, V1, V2, V3, V4, V5, V6, V7, and V8.
Save the vector mask register VMR.
Save the vector count register VCR.
Load the vector length register VLR.
Load the vector register V0 and the scalar register R0 with the arguments for OTS$POWDD.
Call OTS$VPOWDD_R1_V8.
Store result in memory.
Restore all scalar and vector registers except for V0. (The results of the call to OTS$VPOWDD_R1_V8 are stored in V0.)

The following MACRO program fragment shows how to call OTS$VPOWDD_R1_ V8 to compute the result of raising 60 values to the power P. Assume that:

V0 through V8 and R0 and R1 have been saved.
R4 points to the vector of 60 input base values.
R0 and R1 contain the D-floating value P.
R6 points to the location where the results will be stored.
R5 contains the stride.

Note that OTS$VPOWDD_R1_V8 raises a D-floating base to a D-floating power, which you determine from the DD in the routine name. (For further explanation, refer to Section 2.3.3, “Vector Routine Name Format”.) The stride (the number of array elements that are skipped) must be a multiple of 8 because each D-floating value requires 8 bytes.

                               ; R0/R1 already contains the power
MTVLR   #60                    ; Load VLR
MOVL    #8, R5                 ; Stride
VLDQ    (R4), R5, V0           ; Load V0 with the actual arguments
CALLS   #0,G^OTS$VPOWDD_R1_V8  ; CALL OTS$VPOWDD 
VSTQ    V0, (R6), R5           ; Store the results

2.4. Fast-Vector Math Routines

This section describes the fast-vector math routines that offer significantly higher performance at the cost of slightly reduced accuracy when compared with corresponding standard vector math routines. Also note that some fast-vector math routines have restricted argument domains.

When you specify the compile command qualifiers /VECTOR and /MATH_ LIBRARY=FAST, the VSI Fortran compiler selects the appropriate fast-vector math routine, if one exists. The default is /MATH_LIBRARY=ACCURATE. You must specify the /G_FLOATING compile qualifier in conjunction with the /MATH_ LIBRARY=FAST and /VECTOR qualifiers to access the G_floating routines.

You can call these routines from VAX MACRO using the standard calling method. The math function names, together with corresponding entry points of the fast-vector math routines, are listed in Table 2–5.

Table 2.5. Fast-Vector Math Routines

Function Name	Data Type	Call or JSB	Vector Input Registers	Vector Output Registers	Vector Name (Underflows Not Signaled)
ATAN	F_floating	JSB	V0	V0	MTH$VYATAN_R0_V3
DATAN	D_floating	JSB	V0	V0	MTH$VYDATAN_R0_V5
GATAN	G_floating	JSB	V0	V0	MTH$VYGATAN_R0_V5
ATAN2	F_floating	JSB	V0, V1	V0	MTH$VVYATAN2_R0_V5
DATAN2	D_floating	JSB	V0, V1	V0	MTH$VVYDATAN2_R0_V5
GATAN2	G_floating	JSB	V0, V1	V0	MTH$VVYGATAN2_R0_V5
COS	F_floating	JSB	V0	V0	MTH$VYCOS_R0_V3
DCOS	D_floating	JSB	V0	V0	MTH$VYDCOS_R0_V3
GCOS	G_floating	JSB	V0	V0	MTH$VYGCOS_R0_V3
EXP	F_floating	JSB	V0	V0	MTH$VYEXP_R0_V4
DEXP	D_floating	JSB	V0	V0	MTH$VYDEXP_R0_V6
GEXP	G_floating	JSB	V0	V0	MTH$VYGEXP_R0_V6
LOG	F_floating	JSB	V0	V0	MTH$VYALOG_R0_V5
DLOG	D_floating	JSB	V0	V0	MTH$VYDLOG_R0_V5
GLOG	G_floating	JSB	V0	V0	MTH$VYGLOG_R0_V5
LOG10	F_floating	JSB	V0	V0	MTH$VYALOG10_R0_V5
DLOG10	D_floating	JSB	V0	V0	MTH$VYDLOG10_R0_V5
GLOG10	G_floating	JSB	V0	V0	MTH$VYGLOG10_R0_V5
SIN	F_floating	JSB	V0	V0	MTH$VYSIN_R0_V3
DSIN	D_floating	JSB	V0	V0	MTH$VYDSIN_R0_V3
GSIN	G_floating	JSB	V0	V0	MTH$VYGSIN_R0_V3
SQRT	F_floating	JSB	V0	V0	MTH$VYSQRT_R0_V4
DSQRT	D_floating	JSB	V0	V0	MTH$VYDSQRT_R0_V4
GSQRT	G_floating	JSB	V0	V0	MTH$VYGSQRT_R0_V4
TAN	F_floating	JSB	V0	V0	MTH$VYTAN_R0_V3
DTAN	D_floating	JSB	V0	V0	MTH$VYDTAN_R0_V3
GTAN	G_floating	JSB	V0	V0	MTH$VYGTAN_R0_V3
POWRR(X**Y)	F_floating	CALL	V0, R0	V0	OTS$VYPOWRR_R1_V4
POWDD(X**Y)	D_floating	CALL	V0, R0	V0	OTS$VYPOWDD_R1_V8
POWGG(X**Y)	G_floating	CALL	V0, R0	V0	OTS$VYPOWGG_R1_V9

2.4.1. Exception Handling

The fast-vector math routines signal all errors except floating underflow. No intermediate calculations result in exceptions. To optimize performance, the following message signals all errors:

%SYSTEM-F-VARITH, vector arithmetic fault

2.4.2. Special Restrictions On Input Arguments

The special restrictions listed in Table 2–6 apply only to fast-vector routines SIN, COS, and TAN. The standard vector routines handle the full range of VAX floating-point numbers.

Table 2.6. Input Argument Restrictions

Function Name	Input Argument Domain (in Radians)
SIN	~( -6746518783.0, 6746518783.0)
COS	~( -6746518783.0, 6746518783.0)
TAN	~( -3373259391.5, 3373259391.5)

If the application program uses arguments outside of the listed domain, the routine returns the following error message:

%SYSTEM-F-VARITH, vector arithmetic fault

If the application requires argument values beyond the listed limits, use the corresponding standard vector math routine.

2.4.3. Accuracy

The fast-vector math routines do not guarantee the same results as those obtained with the corresponding standard vector math routines. Calls to the fast-vector routines generally yield results that are different from the scalar and original vector MTH$ library routines. The typical maximum error is a 2-LSB (Least Significant Bit) error for the F_floating routines and a 4-LSB error for the D_ floating and G_floating routines. This generally corresponds to a difference in the 6th significant decimal digit for the F_floating routines, the 15th digit for D_floating, and the 14th digit for G_floating.

2.4.4. Performance

The fast-vector math routines generally provide performance improvements over the standard vector routines ranging from 15 to 300 percent, depending on the routines called and input arguments to the routines. The overall performance improvement using fast-vector math routines in a typical user application will increase, but not at the same level as the routines themselves. You should do performance and correctness testing of your application using both the fast-vector and the standard vector math routines before deciding which to use for your application.

Chapter 3. Scalar MTH$ Reference Section

The Scalar MTH$ Reference Section provides detailed descriptions of the scalar routines provided by the OpenVMS RTL Mathematics (MTH$) facility.

MTH$xACOS

MTH$xACOS — Arc Cosine of Angle Expressed in Radians. Given the cosine of an angle, the Arc Cosine of Angle Expressed in Radians routine returns that angle (in radians).

Format

MTH$ACOS cosine

MTH$DACOS cosine

MTH$GACOS cosine

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ACOS_R4

MTH$DACOS_R7

MTH$GACOS_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in radians. The angle returned will have a value in the range:

0 ≤ angle ≤ π

MTH$ACOS returns an F-floating number. MTH$DACOS returns a D-floating number. MTH$GACOS returns a G-floating number.

Argument

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The cosine of the angle whose value (in radians) is to be returned. The cosine argument is the address of a floating-point number that is this cosine. The absolute value of cosine must be less than or equal to 1. For MTH$ACOS, cosine specifies an F-floating number. For MTH$DACOS, cosine specifies a D-floating number. For MTH$GACOS, cosine specifies a G-floating number.

Description

The angle in radians whose cosine is X is computed as:

Value of Cosine	Value Returned
0	π/2
1	0
-1	π
0 < X < 1	zAT AN(zSQRT (l - X²)/X), where zATAN and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
-1 < X < 0	zAT AN(zSQRT (l - X²)/X)+ π
1 < \|X\|	The error MTH$_INVARGMAT is signaled

See MTH$HACOS for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xACOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of cosine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

Examples

100     !+ 
        ! This BASIC program demonstrates the use of 
        ! MTH$ACOS. 
        !- 
 
        EXTERNAL REAL FUNCTION MTH$ACOS 
        DECLARE REAL COS_VALUE, ANGLE 
300     INPUT "Cosine value between -1 and +1 "; COS_VALUE 
400     IF (COS_VALUE < -1) OR (COS_VALUE > 1) 
                THEN PRINT "Invalid cosine value" 
                     GOTO 300 
500     ANGLE = MTH$ACOS( COS_VALUE ) 
        PRINT "The angle with that cosine is "; ANGLE; "radians" 
32767   END

This BASIC program prompts for a cosine value and determines the angle that has that cosine. The output generated by this program is as follows:

$ RUN ACOS
Cosine value between -1 and +1 ?  .5
The angle with that cosine is 1.0472 radians

PROGRAM GETANGLE(INPUT,OUTPUT); 
 
{+} 
{ This Pascal program uses MTH$ACOS to determine 
{ the angle which has the cosine given as input. 
{-} 
 
VAR 
        COS : REAL; 
 
FUNCTION MTH$ACOS(COS : REAL) : REAL; 
        EXTERN; 
 
BEGIN 
        WRITE('Cosine value between -1 and +1:  '); 
        READ (COS); 
        WRITELN('The angle with that cosine is ', MTH$ACOS(COS), 
        ' radians'); 
END.

This Pascal program prompts for a cosine value and determines the angle that has that cosine. The output generated by this program is as follows:

$ RUN ACOS
Cosine value between -1 and +1:  .5
The angle with that cosine is 1.04720E+00 radians

MTH$xACOSD

MTH$xACOSD — Arc Cosine of Angle Expressed in Degrees. Given the cosine of an angle, the Arc Cosine of Angle Expressed in Degrees routine returns that angle (in degrees).

Format

MTH$ACOSD cosine

MTH$DACOSD cosine

MTH$GACOSD cosine

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ACOSD_R4

MTH$DACOSD_R7

MTH$GACOSD_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in degrees. The angle returned will have a value in the range:

0 ≤ angle ≤ 180

MTH$ACOSD returns an F-floating number. MTH$DACOSD returns a D-floating number. MTH$GACOSD returns a G-floating number.

Argument

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Cosine of the angle whose value (in degrees) is to be returned. The cosine argument is the address of a floating-point number that is this cosine. The absolute value of cosine must be less than or equal to 1. For MTH$ACOSD, cosine specifies an F-floating number. For MTH$DACOSD, cosine specifies a D-floating number. For MTH$GACOSD, cosine specifies a G-floating number.

Description

The angle in degrees whose cosine is X is computed as:

Value of Cosine	Angle Returned
0	90
1	0
-1	180
0 < X < 1	zATAND(zSQRT(1-X ²)/X) , where zATAND and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
-1 < X < 0	zATAND(zSQRT(1-X ²)/X) + 180
1 < \|X\|	The error MTH$_INVARGMAT is signaled

See MTH$HACOSD for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xACOSD routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of cosine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

Example

PROGRAM ACOSD(INPUT,OUTPUT); 
{+} 
{ This Pascal program demonstrates the use of MTH$ACOSD. 
{-} 
FUNCTION MTH$ACOSD(COS : REAL): REAL; EXTERN; 
 
VAR 
  COSINE : REAL; 
  RET_STATUS : REAL; 
 
BEGIN 
  COSINE := 0.5; 
  RET_STATUS := MTH$ACOSD(COSINE); 
  WRITELN('The angle, in degrees, is: ', RET_STATUS); 
END.

The output generated by this Pascal example program is as follows:

The angle, expressed in degrees, is:  6.00000E+01

MTH$xASIN

MTH$xASIN — Arc Sine in Radians. Given the sine of an angle, the Arc Sine in Radians routine returns that angle (in radians).

Format

MTH$ASIN sine

MTH$DASIN sine

MTH$GASIN sine

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ASIN_R4

MTH$DASIN_R7

MTH$GASIN_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in radians. The angle returned will have a value in the range:

-π/2 ≤ angle ≤ π/2

MTH$ASIN returns an F-floating number. MTH$DASIN returns a D-floating number. MTH$GASIN returns a G-floating number.

Argument

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The sine of the angle whose value (in radians) is to be returned. The sine argument is the address of a floating-point number that is this sine. The absolute value of sine must be less than or equal to 1. For MTH$ASIN, sine specifies an F-floating number. For MTH$DASIN, sine specifies a D-floating number. For MTH$GASIN, sine specifies a G-floating number.

Description

The angle in radians whose sine is X is computed as:

Value of Sine	Angle Returned
0	0
1	π/2
-1	-π/2
0 < \|X\| < 1	zATAN(X/zSQRT(1-X ²)) , where zATAN and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
1 < \|X\|	The error MTH$_INVARGMAT is signaled

See MTH$HASIN for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xASIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of sine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xASIND

MTH$xASIND — Arc Sine in Degrees. Given the sine of an angle, the Arc Sine in Degrees routine returns that angle (in degrees).

Format

MTH$ASIND sine

MTH$DASIND sine

MTH$GASIND sine

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ASIND_R4

MTH$DASIND_R7

MTH$GASIND_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in degrees. The angle returned will have a value in the range:

-90 ≤ angle ≤ 90

MTH$ASIND returns an F-floating number. MTH$DASIND returns a D-floating number. MTH$GASIND returns a G-floating number.

Argument

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Sine of the angle whose value (in degrees) is to be returned. The sine argument is the address of a floating-point number that is this sine. The absolute value of sine must be less than or equal to 1. For MTH$ASIND, sine specifies an F-floating number. For MTH$DASIND, sine specifies a D-floating number. For MTH$GASIND, sine specifies a G-floating number.

Description

The angle in degrees whose sine is X is computed as:

Value of Cosine	Value Returned
0	0
1	90
-1	-90
0 < \|X\| < 1	zATAND(X/zSQRT(1-X ²)) , where zATAND and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
1 < \|X\|	The error MTH$_INVARGMAT is signaled

See MTH$HASIND for the description of the H-floating version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xASIND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of sine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xATAN

MTH$xATAN — Arc Tangent in Radians. Given the tangent of an angle, the Arc Tangent in Radians routine returns that angle (in radians).

Format

MTH$ATAN tangent

MTH$DATAN tangent

MTH$GATAN tangent

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ATAN_R4

MTH$DATAN_R7

MTH$GATAN_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in radians. The angle returned will have a value in the range:

-π/2 ≤ angle ≤ π/2

MTH$ATAN returns an F-floating number. MTH$DATAN returns a D-floating number. MTH$GATAN returns a G-floating number.

Argument

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The tangent of the angle whose value (in radians) is to be returned. The tangent argument is the address of a floating-point number that is this tangent. For MTH$ATAN, tangent specifies an F-floating number. For MTH$DATAN, tangent specifies a D-floating number. For MTH$GATAN, tangent specifies a G-floating number.

Description

In radians, the computation of the arc tangent function is based on the following identities:

arctan(X) = X - X ³/3 + X ⁵/5 - X ⁷/7 + ...
arctan(X) = X + X*Q(X ²),
where Q(Y) = - Y/3 + Y ²/5 - Y ³/7 + ...
arctan(X) = X*P(X ²),
where P(Y) = 1 - Y/3 + Y ²/5 - Y ³/7 + ...
arctan(X) = π/2 - arctan(1/X)
arctan(X) = arctan(A) + arctan((X-A)/(1+A*X))
for any real A

The angle in radians whose tangent is X is computed as:

Value of Cosine	Angle Returned
0 ≤ X ≤ 3/32	X + X * Q(X ²)
3/32 < X ≤ 11	ATAN(A) + V* (P(V ²)), where A and ATAN(A) are chosen by table lookup and V = (X - A)/(1 + A*X)
11 < X	π/2 - W* (P(W ²)) where W = 1/X
X < 0	-zATAN(\|X\|)

See MTH$HATAN for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xATAN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xATAND

MTH$xATAND — Arc Tangent in Degrees. Given the tangent of an angle, the Arc Tangent in Degrees routine returns that angle (in degrees).

Format

MTH$ATAND tangent

MTH$DATAND tangent

MTH$GATAND tangent

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ATAND_R4

MTH$DATAND_R7

MTH$GATAND_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in degrees. The angle returned will have a value in the range:

-90 ≤ angle ≤ 90

MTH$ATAND returns an F-floating number. MTH$DATAND returns a D-floating number. MTH$GATAND returns a G-floating number.

Argument

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The tangent of the angle whose value (in degrees) is to be returned. The tangent argument is the address of a floating-point number that is this tangent. For MTH$ATAND, tangent specifies an F-floating number. For MTH$DATAND, tangent specifies a D-floating number. For MTH$GATAND, tangent specifies a G-floating number.

Description

The computation of the arc tangent function is based on the following identities:

arctan(X) = (180/π)* (X - X ³/3 + X ⁵/5 - X ⁷/7 + ...)
arctan(X) = 64*X + X*Q(X ²),
where Q(Y) = 180/π*[(1- 64*π/180)] - Y/3 + Y ²/5 - Y ³/7 + Y ⁴/9
arctan(X) = X*P(X ²),
where P(Y) = 180/π*[1 - Y/3 + Y ²/5 - Y ³/7 + Y ⁴/9 ...]
arctan(X) = 90 - arctan(1/X)
arctan(X) = arctan(A) + arctan((X - A)/(1 + A*X))

The angle in degrees whose tangent is X is computed as:

Value of Cosine	Angle Returned
X ≤ 3/32	64X + XQ(X ²)
3/32 < X ≤ 11	ATAND(A) + VP(V ²) , where A and ATAND(A) are chosen by table lookup and V =(X - A)/(1 + AX)
11 < X	90 - W * (P(W ²)), where W = 1/X
X < 0	-zATAND(\|X\|)

See MTH$HATAND for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xATAND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xATAN2

MTH$xATAN2 — Arc Tangent in Radians with Two Arguments. Given sine and cosine , the Arc Tangent in Radians with Two Arguments routine returns the angle (in radians) whose tangent is given by the quotient of sine and cosine (sine /cosine ).

Format

MTH$ATAN2 sine ,cosine

MTH$DATAN2 sine ,cosine

MTH$GATAN2 sine ,cosine

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in radians. MTH$ATAN2 returns an F-floating number. MTH$DATAN2 returns a D-floating number. MTH$GATAN2 returns a G-floating number.

Argument

sine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Dividend. The sine argument is the address of a floating-point number that is this dividend. For MTH$ATAN2, sine specifies an F-floating number. For MTH$DATAN2, sine specifies a D-floating number. For MTH$GATAN2, sine specifies a G-floating number.

cosine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Divisor. The cosine argument is the address of a floating-point number that is this divisor. For MTH$ATAN2, cosine specifies an F-floating number. For MTH$DATAN2, cosine specifies a D-floating number. For MTH$GATAN2, cosine specifies a G-floating number.

Description

The angle in radians whose tangent is Y /X is computed as follows, where f is defined in the description of MTH$zCOSH.

Value of Cosine	Angle Returned
X = 0 or Y/X > 2 ^(f+1)	π/2* (signY)
X > 0 and Y/X ≤ 2 ^(f+1)	zATAN(Y/X)
X < 0 and Y/X ≤ 2 ^(f+1)	π* (signY) + zATAN(Y/X)

See MTH$HATAN2 for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xATAN2 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. Both cosine and sine are zero. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xATAND2

MTH$xATAND2 — Arc Tangent in Degrees with Two Arguments. Given sine and cosine , the Arc Tangent in Degrees with Two Arguments routine returns the angle (in degrees) whose tangent is given by the quotient of sine and cosine (sine /cosine ).

Format

MTH$ATAND2 sine ,cosine

MTH$DATAND2 sine ,cosine

MTH$GATAND2 sine ,cosine

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Angle in degrees. MTH$ATAND2 returns an F-floating number. MTH$DATAND2 returns a D-floating number. MTH$GATAND2 returns a G-floating number.

Argument

sine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Dividend. The sine argument is the address of a floating-point number that is this dividend. For MTH$ATAND2, sine specifies an F-floating number. For MTH$DATAND2, sine specifies a D-floating number. For MTH$GATAND2, sine specifies a G-floating number.

cosine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Divisor. The cosine argument is the address of a floating-point number that is this divisor. For MTH$ATAND2, cosine specifies an F-floating number. For MTH$DATAND2, cosine specifies a D-floating number. For MTH$GATAND2, cosine specifies a G-floating number.

Description

The angle in degrees whose tangent is Y /X is computed below and where f is defined in the description of MTH$zCOSH.

Value of Cosine	Angle Returned
X = 0 or Y/X > 2 ^(f+1)	90* (signY)
X > 0 and Y/X ≤ 2 ^(f+1)	zATAND(Y/X)
X < 0 and Y/X ≤ 2 ^(f+1)	180 * (signY) + zATAND(Y/X)

See MTH$HATAND2 for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xATAND2 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. Both cosine and sine are zero. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xATANH

MTH$xATANH — Hyperbolic Arc Tangent. Given the hyperbolic tangent of an angle, the Hyperbolic Arc Tangent routine returns the hyperbolic arc tangent of that angle.

Format

MTH$ATANH hyperbolic-tangent

MTH$DATANH hyperbolic-tangent

MTH$GATANH hyperbolic-tangent

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The hyperbolic arc tangent of hyperbolic-tangent. MTH$ATANH returns an F-floating number. MTH$DATANH returns a D-floating number. MTH$GATANH returns a G-floating number.

Argument

hyperbolic-tangent

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Hyperbolic tangent of an angle. The hyperbolic-tangent argument is the address of a floating-point number that is this hyperbolic tangent. For MTH$ATANH, hyperbolic-tangent specifies an F-floating number. For MTH$DATANH, hyperbolic-tangent specifies a D-floating number. For MTH$GATANH, hyperbolic-tangent specifies a G-floating number.

Description

The hyperbolic arc tangent function is computed as follows:

Value of Cosine	Value Returned
\|X\| < 1	zATANH(X) = zLOG((1+X)/(1-X))/2
\|X\| ≥ 1	An invalid argument is signaled

See MTH$HATANH for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xATANH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument: \|X\| ≥ 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$CxABS

MTH$CxABS — Complex Absolute Value. The Complex Absolute Value routine returns the absolute value of a complex number (r,i).

Format

MTH$CABS complex-number

MTH$CDABS complex-number

MTH$CGABS complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The absolute value of a complex number. MTH$CABS returns an F-floating number. MTH$CDABS returns a D-floating number. MTH$CGABS returns a G-floating number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex, D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i), where r and i are both floating-point complex values. The complex-number argument is the address of this complex number. For MTH$CABS, complex-number specifies an F-floating complex number. For MTH$CDABS, complex-number specifies a D-floating complex number. For MTH$CGABS, complex-number specifies a G-floating complex number.

Description

The complex absolute value is computed as follows, where MAX is the larger of | r | and | i | , and MIN is the smaller of | r | and | i | :

result = MAX * SQRT((MIN/MAX)² + 1)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CxABS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library when both r and i are large.

Examples

C+ 
C    This Fortran example forms the absolute value of an 
C    F-floating complex number using MTH$CABS and the 
C    Fortran random number generator RAN. 
C 
C    Declare Z as a complex value and MTH$CABS as a REAL*4 value. 
C    MTH$CABS will return the absolute value of Z:   Z_NEW = MTH$CABS(Z). 
C- 
 
        COMPLEX Z 
        COMPLEX CMPLX 
        REAL*4 Z_NEW,MTH$CABS 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the Fortran generic CMPLX. 
C- 
 
        Z = CMPLX(RAN(M),RAN(M)) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and 
C    imaginary part "i". 
C- 
 
       TYPE *, ' The complex number z is',z 
       TYPE *, ' It has real part',REAL(Z),'and imaginary part',AIMAG(Z) 
       TYPE *, ' ' 
 
C+ 
C    Compute the complex absolute value of Z. 
C- 
 
        Z_NEW = MTH$CABS(Z) 
        TYPE *, ' The complex absolute value of',z,' is',Z_NEW 
        END

This example uses an F-floating complex number for complex-number. The output of this Fortran example is as follows:

The complex number z is (0.8535407,0.2043402) 
It has real part  0.8535407    and imaginary part  0.2043402 
 
The complex absolute value of (0.8535407,0.2043402) is  0.8776597

C+ 
C    This Fortran example forms the absolute 
C    value of a G-floating complex number using 
C    MTH$CGABS and the Fortran random number 
C    generator RAN. 
C 
C    Declare Z as a complex value and MTH$CGABS as a 
C    REAL*8 value. MTH$CGABS will return the absolute 
C    value of Z: Z_NEW = MTH$CGABS(Z). 
C- 
 
 
        COMPLEX*16 Z 
        REAL*8 Z_NEW,MTH$CGABS 
 
C+ 
C    Generate a random complex number with the Fortran 
C    generic CMPLX. 
C- 
 
        Z = (12.34567890123,45.536376385345) 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' ' 
 
C+ 
C    Compute the complex absolute value of Z. 
C- 
 
        Z_NEW = MTH$CGABS(Z) 
        TYPE *, ' The complex absolute value of',z,' is',Z_NEW 
        END

This Fortran example uses a G-floating complex number for complex-number. Because this example uses a G-floating number, it must be compiled as follows:

$ Fortran/G MTHEX.FOR

Notice the difference in the precision of the output generated:

The complex number z is (12.3456789012300,45.5363763853450) 
The complex absolute value of (12.3456789012300,45.5363763853450) is 
 47.1802645376230

MTH$CCOS

MTH$CCOS — Cosine of a Complex Number (F-Floating Value). The Cosine of a Complex Number (F-Floating Value) routine returns the cosine of a complex number as an F-floating value.

Format

MTH$CCOS complex-number

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

The complex cosine of the complex input number. MTH$CCOS returns an F-floating complex number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i) where r and i are floating-point numbers. The complex- number argument is the address of this complex number. For MTH$CCOS, complex-number specifies an F-floating complex number.

Description

The complex cosine is calculated as follows:

result = (COS(r) * COSH(i), -SIN(r) * SINH(i))

See MTH$CxCOS for the descriptions of the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CCOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of i is greater than about 88.029 for F-floating values.

Example

C+ 
C    This Fortran example forms the complex 
C    cosine of an F-floating complex number using 
C    MTH$CCOS and the Fortran random number 
C    generator RAN. 
C 
C    Declare Z and MTH$CCOS as complex values. 
C    MTH$CCOS will return the cosine value of 
C    Z:         Z_NEW = MTH$CCOS(Z) 
C- 
 
 
        COMPLEX Z,Z_NEW,MTH$CCOS 
        COMPLEX CMPLX 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the 
C    Fortran generic CMPLX. 
C- 
 
        Z = CMPLX(RAN(M),RAN(M)) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and 
C    imaginary part "i". 
C- 
 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' It has real part',REAL(Z),'and imaginary part',AIMAG(Z) 
        TYPE *, ' ' 
 
C+ 
C    Compute the complex cosine value of Z. 
C- 
 
        Z_NEW = MTH$CCOS(Z) 
        TYPE *, ' The complex cosine value of',z,' is',Z_NEW 
        END

This Fortran example demonstrates the use of MTH$CCOS, using the MTH$CCOS entry point. The output of this program is as follows:

The complex number z is (0.8535407,0.2043402) 
It has real part  0.8535407    and imaginary part  0.2043402 
The complex cosine value of (0.8535407,0.2043402) is (0.6710899,-0.1550672)

MTH$CxCOS

MTH$CxCOS — Cosine of a Complex Number. The Cosine of a Complex Number routine returns the cosine of a complex number.

Format

MTH$CDCOS complex-cosine ,complex-number

MTH$CGCOS complex-cosine ,complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

None.

Argument

complex-cosine

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

Complex cosine of the complex-number. The complex cosine routines that have D-floating and G-floating complex input values write the address of the complex cosine into the complex-cosine argument. For MTH$CDCOS, the complex- cosine argument specifies a D-floating complex number. For MTH$CGCOS, the complex-cosine argument specifies a G-floating complex number.

complex-number

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i) where r and i are floating-point numbers. The complex- number argument is the address of this complex number. For MTH$CDCOS, complex-number specifies a D-floating complex number. For MTH$CGCOS, complex-number specifies a G-floating complex number.

Description

The complex cosine is calculated as follows:

result = (COS(r) * COSH(i), -SIN(r) * SINH(i))

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CxCOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of i is greater than about 88.029 for F-floating and D-floating values, or greater than 709.089 for G-floating values.

Example

C+ 
C    This Fortran example forms the complex 
C    cosine of a D-floating complex number using 
C    MTH$CDCOS and the Fortran random number 
C    generator RAN. 
C 
C    Declare Z and MTH$CDCOS as complex values. 
C    MTH$CDCOS will return the cosine value of 
C    Z:         Z_NEW = MTH$CDCOS(Z) 
C- 
 
 
        COMPLEX*16 Z,Z_NEW,MTH$CDCOS 
        COMPLEX*16 DCMPLX 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the 
C    Fortran generic DCMPLX. 
C- 
 
        Z = DCMPLX(RAN(M),RAN(M)) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and 
C    imaginary part "i". 
C- 
 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' ' 
 
C+ 
C    Compute the complex cosine value of Z. 
C- 
 
        Z_NEW = MTH$CDCOS(Z) 
        TYPE *, ' The complex cosine value of',z,' is',Z_NEW 
        END

This Fortran example program demonstrates the use of MTH$CxCOS, using the MTH$CDCOS entry point. Notice the high precision of the output generated:

The complex number z is (0.8535407185554504,0.2043401598930359) 
The complex cosine value of (0.8535407185554504,0.2043401598930359) is 
 (0.6710899028500762,-0.1550672019621661)

MTH$CEXP

MTH$CEXP — Complex Exponential (F-Floating Value). The Complex Exponential (F-Floating Value) routine returns the complex exponential of a complex number as an F-floating value.

Format

MTH$CEXP complex-number

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

Complex exponential of the complex input number. MTH$CEXP returns an F-floating complex number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex
access:	read only
mechanism:	by reference

Complex number whose complex exponential is to be returned. This complex number has the form (r,i), where r is the real part and i is the imaginary part. The complex-number argument is the address of this complex number. For MTH$CEXP, complex-number specifies an F-floating number.

Description

The complex exponential is computed as follows:

complex-exponent = (EXP(r)*COS(i), EXP(r)*SIN(i))

See MTH$CxEXP for the descriptions of the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CEXP routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of r is greater than about 88.029 for F-floating values.

Example

C+ 
C    This Fortran example forms the complex exponential 
C    of an F-floating complex number using MTH$CEXP 
C    and the Fortran random number generator RAN. 
C 
C    Declare Z and MTH$CEXP as complex values. MTH$CEXP 
C    will return the exponential value of Z: Z_NEW = MTH$CEXP(Z) 
C- 
 
        COMPLEX Z,Z_NEW,MTH$CEXP 
        COMPLEX CMPLX 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the 
C    Fortran generic CMPLX. 
C- 
 
        Z = CMPLX(RAN(M),RAN(M)) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" 
C    and imaginary part "i". 
C- 
 
       TYPE *, ' The complex number z is',z 
       TYPE *, ' It has real part',REAL(Z),'and imaginary part',AIMAG(Z) 
       TYPE *, ' ' 
 
C+ 
C    Compute the complex exponential value of Z. 
C- 
 
        Z_NEW = MTH$CEXP(Z) 
        TYPE *, ' The complex exponential value of',z,' is',Z_NEW 
        END

This Fortran program demonstrates the use of MTH$CEXP as a function call. The output generated by this example is as follows:

The complex number z is (0.8535407,0.2043402) 
It has real part  0.8535407    and imaginary part  0.2043402 
The complex exponential value of (0.8535407,0.2043402) is 
 (2.299097,0.4764476)

MTH$CxEXP

MTH$CxEXP — Complex Exponential. The Complex Exponential routine returns the complex exponential of a complex number.

Format

MTH$CDEXP complex-exponent ,complex-number

MTH$CGEXP complex-exponent ,complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

None.

Argument

complex-exponent

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

Complex exponential of complex-number. The complex exponential routines that have D-floating complex and G-floating complex input values write the complex-exponent into this argument. For MTH$CDEXP, complex-exponent argument specifies a D-floating complex number. For MTH$CGEXP, complex-exponent specifies a G-floating complex number.

complex-number

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

Complex number whose complex exponential is to be returned. This complex number has the form (r,i), where r is the real part and i is the imaginary part. The complex-number argument is the address of this complex number. For MTH$CDEXP, complex-number specifies a D-floating number. For MTH$CGEXP, complex-number specifies a G-floating number.

Description

The complex exponential is computed as follows:

complex-exponent = (EXP(r)*COS(i), EXP(r)*SIN(i))

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CxEXP routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of r is greater than about 88.029 for D-floating values, or greater than about 709.089 for G-floating values.

Example

C+ 
C    This Fortran example forms the complex exponential 
C    of a G-floating complex number using MTH$CGEXP 
C    and the Fortran random number generator RAN. 
C 
C    Declare Z and MTH$CGEXP as complex values. 
C    MTH$CGEXP will return the exponential value 
C    of Z:      CALL MTH$CGEXP(Z_NEW,Z) 
C- 
 
        COMPLEX*16 Z,Z_NEW 
        COMPLEX*16 MTH$GCMPLX 
        REAL*8 R,I 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the Fortran 
C-   generic CMPLX. 
C- 
 
        R = RAN(M) 
        I = RAN(M) 
        Z = MTH$GCMPLX(R,I) 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' ' 
 
C+ 
C    Compute the complex exponential value of Z. 
C- 
 
        CALL MTH$CGEXP(Z_NEW,Z) 
        TYPE *, ' The complex exponential value of',z,' is',Z_NEW 
        END

This Fortran example demonstrates how to access MTH$CGEXP as a procedure call. Because G-floating numbers are used, this program must be compiled using the command "Fortran/G filename".

Notice the high precision of the output generated:

 The complex number z is (0.853540718555450,0.204340159893036) 
 The complex exponential value of (0.853540718555450,0.204340159893036) is 
(2.29909677719458,0.476447678044977)

MTH$CLOG

MTH$CLOG — Complex Natural Logarithm (F-Floating Value). The Complex Natural Logarithm (F-Floating Value) routine returns the complex natural logarithm of a complex number as an F-floating value.

Format

MTH$CLOG complex-number

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

The complex natural logarithm of a complex number. MTH$CLOG returns an F-floating complex number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex
access:	read only
mechanism:	by reference

Complex number whose complex natural logarithm is to be returned. This complex number has the form (r,i), where r is the real part and i is the imaginary part. The complex-number argument is the address of this complex number. For MTH$CLOG, complex-number specifies an F-floating number.

Description

The complex natural logarithm is computed as follows:

CLOG(x) = (LOG(CABS(x)), ATAN2(i,r))

See MTH$CxLOG for the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$CLOG routine encountered a floating-point reserved operand (a floating-point datum with a sign bit of 1 and a biased exponent of 0) due to incorrect user input. Floating-point reserved operands are reserved for use by VSI.

Example

See Section 1.7.4, “MACRO Examples” for examples of using MTH$CLOG from VAX MACRO.

MTH$CxLOG

MTH$CxLOG — Complex Natural Logarithm. The Complex Natural Logarithm routine returns the complex natural logarithm of a complex number.

Format

MTH$CDLOG complex-natural-log ,complex-number

MTH$CGLOG complex-natural-log ,complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

None.

Argument

complex-natural-log

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

Natural logarithm of the complex number specified by complex-number. The complex natural logarithm routines that have D-floating complex and G-floating complex input values write the address of the complex natural logarithm into complex-natural-log. For MTH$CDLOG, the complex-natural-log argument specifies a D-floating complex number. For MTH$CGLOG, the complex-natural-log argument specifies a G-floating complex number.

complex-number

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

Complex number whose complex natural logarithm is to be returned. This complex number has the form (r,i), where r is the real part and i is the imaginary part. The complex-number argument is the address of this complex number. For MTH$CDLOG, complex-number specifies a D-floating number. For MTH$CGLOG, complex-number specifies a G-floating number.

Description

The complex natural logarithm is computed as follows:

CLOG(x) = (LOG(CABS(x)), ATAN2(i,r))

Condition Values Signaled

SS$_FLTOVF_F	Floating point overflow can occur. This condition value is signaled from MTH$CxABS when MTH$CxABS overflows.
SS$_ROPRAND	Reserved operand. The MTH$CxLOG routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument: r = i = 0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

Example

C+ 
C   This Fortran example forms the complex logarithm of a D-floating complex 
C   number by using MTH$CDLOG and the Fortran random number generator RAN. 
C 
C   Declare Z and MTH$CDLOG as complex values. Then MTH$CDLOG 
c   returns the logarithm of Z: CALL MTH$CDLOG(Z_NEW,Z). 
C 
C   Declare Z, Z_LOG, MTH$DCMPLX as complex values, and R, I as real values. 
C   MTH$DCMPLX takes two real arguments and returns one complex number. 
C 
C   Given complex number Z, MTH$CDLOG(Z) returns the complex natural 
C   logarithm of Z. 
C- 
        COMPLEX*16 Z,Z_NEW,MTH$DCMPLX 
        REAL*8 R,I 
        R = 3.1425637846746565 
        I = 7.43678469887 
        Z = MTH$DCMPLX(R,I) 
C+ 
C   Z is a complex number (r,i) with real part "r" and imaginary part "i". 
C- 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' ' 
        CALL MTH$CDLOG(Z_NEW,Z) 
        TYPE *,' The complex logarithm of',z,' is',Z_NEW 
        END

This Fortran example program uses MTH$CDLOG by calling it as a procedure. The output generated by this program is as follows:

The complex number z is (3.142563784674657,7.436784698870000) 
The complex logarithm of (3.142563784674657,7.436784698870000) is 
 (2.088587642177504,1.170985519274141)

MTH$CMPLX

MTH$CMPLX — Complex Number Made from F-Floating Point. The Complex Number Made from F-Floating Point routine returns a complex number from two floating-point input values.

Format

MTH$CMPLX real-part ,imaginary-part

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

A complex number. MTH$CMPLX returns an F-floating complex number.

Argument

real-part

OpenVMS usage:	floating_point
type:	F_floating
access:	read only
mechanism:	by reference

Real part of a complex number. The real-part argument is the address of a floating-point number that contains this real part, r, of (r,i). For MTH$CMPLX, real-part specifies an F-floating number.

imaginary-part

OpenVMS usage:	floating_point
type:	F_floating
access:	read only
mechanism:	by reference

Imaginary part of a complex number. The imaginary-part argument is the address of a floating-point number that contains this imaginary part, i, of (r,i). For MTH$CMPLX, imaginary-part specifies an F-floating number.

Description

The MTH$CMPLX routine returns a complex number from two F-floating input values. See MTH$xCMPLX for the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$CMPLX routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

C+ 
C    This Fortran example forms two F-floating 
C    point complex numbers using MTH$CMPLX 
C    and the Fortran random number generator RAN. 
C 
C    Declare Z and MTH$CMPLX as complex values, and R 
C    and I as real values.  MTH$CMPLX takes two real 
C    F-floating point values and returns one COMPLEX*8 number. 
C 
C    Note, since CMPLX is a generic name in Fortran, it would be 
C    sufficient to use CMPLX. 
C    CMPLX must be declared to be of type COMPLEX*8. 
C 
C    Z = CMPLX(R,I) 
C- 
 
 
        COMPLEX Z,MTH$CMPLX,CMPLX 
        REAL*4 R,I 
        INTEGER M 
        M = 1234567 
        R = RAN(M) 
        I = RAN(M) 
        Z = MTH$CMPLX(R,I) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and 
C    imaginary part "i". 
C- 
 
        TYPE *, ' The two input values are:',R,I 
        TYPE *, ' The complex number z is',z 
        z = CMPLX(RAN(M),RAN(M)) 
        TYPE *, ' ' 
        TYPE *, ' Using the Fortran generic CMPLX with random R and I:' 
        TYPE *, ' The complex number z is',z 
        END

This Fortran example program demonstrates the use of MTH$CMPLX. The output generated by this program is as follows:

The two input values are:  0.8535407      0.2043402 
The complex number z is (0.8535407,0.2043402) 
Using the Fortran generic CMPLX with random R and I: 
The complex number z is (0.5722565,0.1857677)

MTH$xCMPLX

MTH$xCMPLX — Complex Number Made from D- or G-Floating Point. The Complex Number Made from D- or G-Floating Point routines return a complex number from two D- or G-floating input values.

Format

MTH$DCMPLX complx ,real-part ,imaginary-part

MTH$GCMPLX complx ,real-part ,imaginary-part

Each of the above formats accepts one of floating-point complex types as input.

Returns

None.

Argument

complx

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

The floating-point complex value of a complex number. The complex exponential functions that have D-floating complex and G-floating complex input values write the address of this floating-point complex value into complx. For MTH$DCMPLX, complx specifies a D-floating complex number. For MTH$GCMPLX, complx specifies a G-floating complex number. For MTH$CMPLX, complx is not used.

real-part

OpenVMS usage:	floating_point
type:	D_floating, G_floating
access:	read only
mechanism:	by reference

Real part of a complex number. The real-part argument is the address of a floating-point number that contains this real part, r, of (r,i). For MTH$DCMPLX, real-part specifies a D-floating number. For MTH$GCMPLX, real-part specifies a G-floating number.

imaginary-part

OpenVMS usage:	floating_point
type:	D_floating, G_floating
access:	read only
mechanism:	by reference

Imaginary part of a complex number. The imaginary-part argument is the address of a floating-point number that contains this imaginary part, i, of (r,i). For MTH$DCMPLX, imaginary-part specifies a D-floating number. For MTH$GCMPLX, imaginary-part specifies a G-floating number.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xCMPLX routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

C+ 
C    This Fortran example forms two D-floating 
C    point complex numbers using MTH$CMPLX 
C    and the Fortran random number generator RAN. 
C 
C    Declare Z and MTH$DCMPLX as complex values, and R 
C    and I as real values.  MTH$DCMPLX takes two real 
C    D-floating point values and returns one 
C    COMPLEX*16 number. 
C 
C- 
 
        COMPLEX*16 Z 
        REAL*8 R,I 
        INTEGER M 
        M = 1234567 
        R = RAN(M) 
        I = RAN(M) 
        CALL MTH$DCMPLX(Z,R,I) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and imaginary 
C    part "i". 
C- 
 
        TYPE *, ' The two input values are:',R,I 
        TYPE *, ' The complex number z is',Z 
        END

This Fortran example demonstrates how to make a procedure call to MTH$DCMPLX. Notice the difference in the precision of the output generated.

The two input values are:  0.8535407185554504      0.2043401598930359 
The complex number z is (0.8535407185554504,0.2043401598930359)

MTH$CONJG

MTH$CONJG — Conjugate of a Complex Number (F-Floating Value). The Conjugate of a Complex Number (F-Floating Value) routine returns the complex conjugate (r,-i) of a complex number (r,i) as an F-floating value.

Format

MTH$CONJG complex-number

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

Complex conjugate of a complex number. MTH$CONJG returns an F-floating complex number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i), where r and i are floating-point numbers. The complex-number argument is the address of this floating-point complex number. For MTH$CONJG, complex-number specifies an F-floating number.

Description

The MTH$CONJG routine returns the complex conjugate (r,-i) of a complex number (r,i) as an F-floating value.

See MTH$xCONJG for the descriptions of the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$CONJG routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xCONJG

MTH$xCONJG — Conjugate of a Complex Number. The Conjugate of a Complex Number routine returns the complex conjugate (r,-i) of a complex number (r,i).

Format

MTH$DCONJG complex-conjugate ,complex-number

MTH$GCONJG complex-conjugate ,complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

None.

Argument

complex-conjugate

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

The complex conjugate (r,-i) of the complex number specified by complex-number. MTH$DCONJG and MTH$GCONJG write the address of this complex conjugate into complex-conjugate. For MTH$DCONJG, the complex-conjugate argument specifies the address of a D-floating complex number. For MTH$GCONJG, the complex-conjugate argument specifies the address of a G-floating complex number.

complex-number

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i), where r and i are floating-point numbers. The complex-number argument is the address of this floating-point complex number. For MTH$DCONJG, complex-number specifies a D-floating number. For MTH$GCONJG, complex-number specifies a G-floating number.

Description

The MTH$xCONJG routines return the complex conjugate (r,-i) of a complex number (r,i).

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xCONJG routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

C+ 
C    This Fortran example forms the complex conjugate 
C    of a G-floating complex number using MTH$GCONJG 
C    and the Fortran random number generator RAN. 
C 
C    Declare Z, Z_NEW, and MTH$GCONJG as a complex values. 
C    MTH$GCONJG will return the complex conjugate 
C    value of Z:   Z_NEW = MTH$GCONJG(Z). 
C- 
        COMPLEX*16 Z,Z_NEW,MTH$GCONJG 
        COMPLEX*16 MTH$GCMPLX 
        REAL*8 R,I,MTH$GREAL,MTH$GIMAG 
        INTEGER M 
        M = 1234567 
C+ 
C    Generate a random complex number with the Fortran generic CMPLX. 
C- 
        R = RAN(M) 
        I = RAN(M) 
        Z = MTH$GCMPLX(R,I) 
        TYPE *, ' The complex number z is',z 
        TYPE 1,MTH$GREAL(Z),MTH$GIMAG(Z) 
   1    FORMAT(' with real part ',F20.16,' and imaginary part',F20.16) 
        TYPE *, ' ' 
C+ 
C    Compute the complex absolute value of Z. 
C- 
        Z_NEW = MTH$GCONJG(Z) 
        TYPE *, ' The complex conjugate value of',z,' is',Z_NEW 
        TYPE 1,MTH$GREAL(Z_NEW),MTH$GIMAG(Z_NEW) 
        END

This Fortran example demonstrates how to make a function call to MTH$GCONJG. Because G-floating numbers are used, the examples must be compiled with the statement "Fortran/G filename".

The output generated by this program is as follows:

The complex number z is (0.853540718555450,0.204340159893036) 
  with real part   0.8535407185554504 
  and imaginary part  0.2043401598930359 
 
The complex conjugate value of     
  (0.853540718555450,0.204340159893036) is 
  (0.853540718555450,-0.204340159893036) 
  with real part   0.8535407185554504  
  and imaginary part -0.2043401598930359

MTH$xCOS

MTH$xCOS — Cosine of Angle Expressed in Radians. The Cosine of Angle Expressed in Radians routine returns the cosine of a given angle (in radians).

Format

MTH$COS angle-in-radians

MTH$DCOS angle-in-radians

MTH$GCOS angle-in-radians

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$COS_R4

MTH$DCOS_R7

MTH$GCOS_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Cosine of the angle. MTH$COS returns an F-floating number. MTH$DCOS returns a D-floating number. MTH$GCOS returns a G-floating number.

Argument

angle-in-radians

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The angle in radians. The angle-in-radians argument is the address of a floating-point number. For MTH$COS, angle-in-radians is an F-floating number. For MTH$DCOS, angle-in-radians specifies a D-floating number. For MTH$GCOS, angle-in-radians specifies a G-floating number.

Description

See MTH$xSINCOS for the algorithm used to compute the cosine.

See MTH$HCOS for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xCOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xCOSD

MTH$xCOSD — Cosine of Angle Expressed in Degrees. The Cosine of Angle Expressed in Degrees routine returns the cosine of a given angle (in degrees).

Format

MTH$COSD angle-in-degrees

MTH$DCOSD angle-in-degrees

MTH$GCOSD angle-in-degrees

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$COSD_R4

MTH$DCOSD_R7

MTH$GCOSD_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Cosine of the angle. MTH$COSD returns an F-floating number. MTH$DCOSD returns a D-floating number. MTH$GCOSD returns a G-floating number.

Argument

angle-in-degrees

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Angle (in degrees). The angle-in-degrees argument is the address of a floating-point number. For MTH$COSD, angle-in-degrees specifies an F-floating number. For MTH$DCOSD, angle-in-degrees specifies a D-floating number. For MTH$GCOSD, angle-in-degrees specifies a G-floating number.

Description

See MTH$xSINCOS for the algorithm used to compute the cosine.

See MTH$HCOSD for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xCOSD routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xCOSH

MTH$xCOSH — Hyperbolic Cosine. The Hyperbolic Cosine routine returns the hyperbolic cosine of the input value.

Format

MTH$COSH floating-point-input-value

MTH$DCOSH floating-point-input-value

MTH$GCOSH floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The hyperbolic cosine of the input value floating-point-input-value. MTH$COSH returns an F-floating number. MTH$DCOSH returns a D-floating number. MTH$GCOSH returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of this input value. For MTH$COSH, floating-point-input-value specifies an F-floating number. For MTH$DCOSH, floating-point-input-value specifies a D-floating number. For MTH$GCOSH, floating-point-input-value specifies a G-floating number.

Description

Computation of the hyperbolic cosine depends on the magnitude of the input argument. The range of the function is partitioned using four data-type- dependent constants: a(z), b(z), and c(z). The subscript z indicates the data type. The constants depend on the number of exponent bits (e ) and the number of fraction bits (f ) associated with the data type (z ).

The values of e and f are:

z	e	f
F	8	24
D	8	56
G	11	53

The values of the constants in terms of e and f are:

Variable	Value
a(z)	2 ^(-f/2)
b(z)	CEILING[ (f+1)/2*ln(2) ]
c(z)	(2 ^e-1)*ln(2)

Based on the above definitions, zCOSH(X) is computed as follows:

Value of X	Value Returned
\|X\| < a(z)	1
a(z) ≤ \|X\| < .25	Computed using a power series expansion in \|X\| ²
.25 ≤ \|X\| < b(z)	(zEXP(\|X\|) + 1/zEXP(\|X\|))/2
b(z) ≤ \|X\| < c(z)	zEXP(\|X\|)/2
c(z) ≤ \|x\|	Overflow occurs

See MTH$HCOSH for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xCOSH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of floating-point-input-value is greater than about yyy; LIB$SIGNAL copies the reserved operand to the signal mechanism vector. The result is the reserved operand -0.0 unless a condition handler changes the signal mechanism vector. The values of yyy are: MTH$COSH---88.722MTH$DCOSH---88.722MTH$GCOSH---709.782

MTH$CSIN

MTH$CSIN — Sine of a Complex Number (F-Floating Value). The Sine of a Complex Number (F-Floating Value) routine returns the sine of a complex number (r,i) as an F-floating value.

Format

MTH$CSIN complex-number

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

Complex sine of the complex number. MTH$CSIN returns an F-floating complex number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i), where r and i are floating-point numbers. The complex-number argument is the address of this complex number. For MTH$CSIN, complex-number specifies an F-floating complex number.

Description

The complex sine is computed as follows:

complex-sine = (SIN(r) * COSH(i), COS(r) * SINH(i))

See MTH$CxSIN for the descriptions of the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CSIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of i is greater than about 88.029 for F-floating values.

MTH$CxSIN

MTH$CxSIN — Sine of a Complex Number. The Sine of a Complex Number routine returns the sine of a complex number (r,i).

Format

MTH$CDSIN complex-sine ,complex-number

MTH$CGSIN complex-sine ,complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

None.

Argument

complex-sine

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

Complex sine of the complex number. The complex sine routines with D-floating complex and G-floating complex input values write the complex sine into this complex-sine argument. For MTH$CDSIN, complex-sine specifies a D-floating complex number. For MTH$CGSIN, complex-sine specifies a G-floating complex number.

complex-number

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

A complex number (r,i), where r and i are floating-point numbers. The complex-number argument is the address of this complex number. For MTH$CDSIN, complex-number specifies a D-floating complex number. For MTH$CGSIN, complex-number specifies a G-floating complex number.

Description

The complex sine is computed as follows:

complex-sine = (SIN(r) * COSH(i), COS(r) * SINH(i))

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CxSIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of i is greater than about 88.029 for D-floating values, or greater than about 709.089 for G-floating values.

Example

C+ 
C    This Fortran example forms the complex sine of a G-floating 
C    complex number using MTH$CGSIN and the Fortran random number 
C    generator RAN. 
C 
C    Declare Z and MTH$CGSIN as complex values.  MTH$CGSIN returns 
C    the sine value of Z:      CALL MTH$CGSIN(Z_NEW,Z) 
C- 
        COMPLEX*16 Z,Z_NEW 
        COMPLEX*16 DCMPLX 
        REAL*8 R,I 
        INTEGER M 
        M = 1234567 
C+ 
C    Generate a random complex number with the 
C    Fortran generic DCMPLX. 
C- 
        R = RAN(M) 
        I = RAN(M) 
        Z = DCMPLX(R,I) 
C+ 
C     Z is a complex number (r,i) with real part "r" and 
C     imaginary part "i". 
C- 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' ' 
C+ 
C    Compute the complex sine value of Z. 
C- 
        CALL MTH$CGSIN(Z_NEW,Z) 
        TYPE *, ' The complex sine value of',z,' is',Z_NEW 
        END

This Fortran example demonstrates a procedure call to MTH$CGSIN. Because this program uses G-floating numbers, it must be compiled with the statement "Fortran/G filename".

The output generated by this program is as follows:

The complex number z is (0.853540718555450,0.204340159893036) 
The complex sine value of (0.853540718555450,0.204340159893036) is 
 (0.769400835484975,0.135253340912255)

MTH$CSQRT

MTH$CSQRT — Complex Square Root (F-Floating Value). The Complex Square Root (F-Floating Value) routine returns the complex square root of a complex number (r,i).

Format

MTH$CSQRT complex-number

Returns

OpenVMS usage:	complex_number
type:	F_floating complex
access:	write only
mechanism:	by value

The complex square root of the complex-number argument. MTH$CSQRT returns an F-floating number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex
access:	read only
mechanism:	by reference

Complex number (r,i). The complex-number argument contains the address of this complex number. For MTH$CSQRT, complex-number specifies an F-floating number.

Description

The complex square root is computed as follows.

First, calculate ROOT and Q using the following equations:

ROOT = SQRT((ABS(r) + CABS(r,i))/2) Q = i/(2 * ROOT)

Then, the complex result is given as follows:

r	i	CSQRT((r,i))
≥0	Any	(ROOT,Q)
<0	≥0	(Q,ROOT)
<0	<0	(-Q,-ROOT)

See MTH$CxSQRT for the descriptions of the D- and G-floating point versions of this routine.

Condition Values Signaled

SS$_FLTOVF_F	Floating point overflow can occur.
SS$_ROPRAND	Reserved operand. The MTH$CSQRT routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$CxSQRT

MTH$CxSQRT — Complex Square Root. The Complex Square Root routine returns the complex square root of a complex number (r,i).

Format

MTH$CDSQRT complex-square-root ,complex-number

MTH$CGSQRT complex-square-root ,complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

None.

Argument

complex-square-root

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	write only
mechanism:	by reference

Complex square root of the complex number specified by complex-number. The complex square root routines that have D-floating complex and G-floating complex input values write the complex square root into complex-square-root. For MTH$CDSQRT, complex-square-root specifies a D-floating complex number. For MTH$CGSQRT, complex-square-root specifies a G-floating complex number.

complex-number

OpenVMS usage:	complex_number
type:	D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

Complex number (r,i). The complex-number argument contains the address of this complex number. For MTH$CDSQRT, complex-number specifies a D-floating number. For MTH$CGSQRT, complex-number specifies a G-floating number.

Description

The complex square root is computed as follows.

First, calculate ROOT and Q using the following equations:

ROOT = SQRT((ABS(r) + CABS(r,i))/2) Q = i/(2 * ROOT)

Then, the complex result is given as follows:

r	i	CSQRT((r,i))
≥0	any	(ROOT,Q)
<0	≥0	(Q,ROOT)
<0	<0	(-Q,-ROOT)

Condition Values Signaled

SS$_FLTOVF_F	Floating point overflow can occur.
SS$_ROPRAND	Reserved operand. The MTH$CxSQRT routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

C+ 
C    This Fortran example forms the complex square root of a D-floating 
C    complex number using MTH$CDSQRT and the Fortran random number 
C    generator RAN. 
C 
C    Declare Z and Z_NEW as complex values. MTH$CDSQRT returns the 
C    complex square root of Z:   CALL MTH$CDSQRT(Z_NEW,Z). 
C- 
        COMPLEX*16 Z,Z_NEW 
        COMPLEX*16 DCMPLX 
        INTEGER M 
        M = 1234567 
C+ 
C    Generate a random complex number with the 
C    Fortran generic CMPLX. 
C- 
        Z = DCMPLX(RAN(M),RAN(M)) 
C+ 
C    Z is a complex number (r,i) with real part "r" and imaginary 
C    part "i". 
C- 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' ' 
C+ 
C    Compute the complex complex square root of Z. 
C- 
        CALL MTH$CDSQRT(Z_NEW,Z) 
        TYPE *, ' The complex square root of',z,' is',Z_NEW 
       END

This Fortran example program demonstrates a procedure call to MTH$CDSQRT. The output generated by this program is as follows:

 The complex number z is (0.8535407185554504,0.2043401598930359) 
 The complex square root of (0.8535407185554504,0.2043401598930359) is 
(0.9303763973040062,0.1098158554350485)

MTH$CVT_x_x

MTH$CVT_x_x — Convert One Double-Precision Value. The Convert One Double-Precision Value routines convert one double-precision value to the destination data type and return the result as a function value. MTH$CVT_D_G converts a D-floating value to G-floating and MTH$CVT_G_D converts a G-floating value to a D-floating value.

Format

MTH$CVT_D_G floating-point-input-val

MTH$CVT_G_D floating-point-input-val

Returns

OpenVMS usage:	floating_point
type:	G_floating, D_floating
access:	write only
mechanism:	by value

The converted value. MTH$CVT_D_G returns a G-floating value. MTH$CVT_G_D returns a D-floating value.

Argument

floating-point-input-val

OpenVMS usage:	floating_point
type:	D_floating, G_floating
access:	read only
mechanism:	by reference

The input value to be converted. The floating-point-input-val argument is the address of this input value. For MTH$CVT_D_G, the floating-point- input-val argument specifies a D-floating number. For MTH$CVT_G_D, the floating-point-input-val argument specifies a G-floating number.

Description

These routines are designed to function as hardware conversion instructions. They fault on reserved operands. If floating-point overflow is detected, an error is signaled. If floating-point underflow is detected and floating-point underflow is enabled, an error is signaled.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CVT_x_x routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library.

MTH$CVT_xA_xA

MTH$CVT_xA_xA — Convert an Array of Double-Precision Values. The Convert an Array of Double-Precision Values routines convert a contiguous array of double-precision values to the destination data type and return the results as an array. MTH$CVT_DA_GA converts D-floating values to G-floating and MTH$CVT_GA_DA converts G-floating values to D-floating.

Format

MTH$CVT_DA_GA floating-point-input-array ,floating-point-dest-array [,array-size] MTH$CVT_GA_DA floating-point-input-array ,floating-point-dest-array [,array-size]

Returns

MTH$CVT_DA_GA and MTH$CVT_GA_DA return the address of the output array to the floating-point-dest-array argument.

Argument

floating-point-input-array

OpenVMS usage:	floating_point
type:	D_floating, G_floating
access:	read only
mechanism:	by reference, array reference

Input array of values to be converted. The floating-point-input-array argument is the address of an array of floating-point numbers. For MTH$CVT_DA_GA, floating-point-input-array specifies an array of D-floating numbers. For MTH$CVT_GA_DA, floating-point-input-array specifies an array of G-floating numbers.

floating-point-dest-array

OpenVMS usage:	floating_point
type:	G_floating, D_floating
access:	write only
mechanism:	by reference, array reference

Output array of converted values. The floating-point-dest-array argument is the address of an array of floating-point numbers. For MTH$CVT_DA_GA, floating-point-dest-array specifies an array of G-floating numbers. For MTH$CVT_GA_DA, floating-point-dest-array specifies an array of D-floating numbers.

array-size

OpenVMS usage:	longword_signed
type:	longword (signed)
access:	read only
mechanism:	by reference

Number of array elements to be converted. The default value is 1. The array-size argument is the address of a longword containing this number of elements.

Description

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$CVT_xA_xA routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library.

MTH$xEXP

MTH$xEXP — Exponential. The Exponential routine returns the exponential of the input value.

Format

MTH$EXP floating-point-input-value

MTH$DEXP floating-point-input-value

MTH$GEXP floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$EXP_R4

MTH$DEXP_R6

MTH$GEXP_R6

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The exponential of floating-point-input-value. MTH$EXP returns an F-floating number. MTH$DEXP returns a D-floating number. MTH$GEXP returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number. For MTH$EXP, floating-point-input-value specifies an F-floating number. For MTH$DEXP, floating-point-input-value specifies a D-floating number. For MTH$GEXP, floating-point-input-value specifies a G-floating number.

Description

The exponential of x is computed as:

Value of x	Value Returned
X > c(z)	Overflow occurs
X ≤ -c(z)	0
\|X\| < 2 ^-(f+1)	1
Otherwise	2 ^Y * 2 ^U * 2 ^W

where: Y = INTEGER(x*ln2(E)) V = FRAC(x*ln2(E)) * 16 U = INTEGER(V)/16 W = FRAC(V)/16 2^W = polynomial approximation of degree 4, 8, or 8 for z = F, D, or G.

See also MTH$xCOSH for definitions of f and c(z).

See MTH$HEXP for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xEXP routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$_FLOOVEMAT

Floating-point overflow in Math Library: floating-point-input-value is greater than yyy; LIB$SIGNAL copies the reserved operand to the signal mechanism vector. The result is the reserved operand -0.0 unless a condition handler changes the signal mechanism vector.

The values of yyy are approximately:

MTH$EXP---88.029
MTH$DEXP---88.029
MTH$GEXP---709.089

MTH$_FLOUNDMAT

Floating-point underflow in Math Library: floating-point-input-value is less than or equal to yyy and the caller (CALL or JSB) has set hardware floating-point underflow enable. The result is set to 0.0. If the caller has not enabled floating-point underflow (the default), a result of 0.0 is returned but no error is signaled.

The values of yyy are approximately:

MTH$EXP--- -- 88.722
MTH$DEXP--- -- 88.722
MTH$GEXP--- -- 709.774

Example

IDENTIFICATION DIVISION. 
PROGRAM-ID.    FLOATING_POINT. 
* 
*  Calls MTH$EXP using a Floating Point data type. 
*  Calls MTH$DEXP using a Double Floating Point data type. 
* 
ENVIRONMENT DIVISION. 
DATA DIVISION. 
WORKING-STORAGE SECTION. 
01 FLOAT_PT     COMP-1. 
01 ANSWER_F     COMP-1. 
01 DOUBLE_PT    COMP-2. 
01 ANSWER_D     COMP-2. 
PROCEDURE DIVISION. 
P0. 
        MOVE 12.34 TO FLOAT_PT. 
        MOVE 3.456 TO DOUBLE_PT. 
 
        CALL "MTH$EXP" USING BY REFERENCE FLOAT_PT GIVING ANSWER_F. 
        DISPLAY " MTH$EXP of ", FLOAT_PT CONVERSION, " is ", 
                                               ANSWER_F CONVERSION. 
 
        CALL "MTH$DEXP" USING BY REFERENCE DOUBLE_PT GIVING ANSWER_D. 
        DISPLAY " MTH$DEXP of ", DOUBLE_PT CONVERSION, " is ", 
                                               ANSWER_D CONVERSION . 
        STOP RUN.

This sample program demonstrates calls to MTH$EXP and MTH$DEXP from COBOL.

The output generated by this program is as follows:

MTH$EXP of  1.234000E+01 is  2.286620E+05 
MTH$DEXP of  3.456000000000000E+00 is 
3.168996280537917E+01

MTH$HACOS

MTH$HACOS — Arc Cosine of Angle Expressed in Radians (H-Floating Value). Given the cosine of an angle, the Arc Cosine of Angle Expressed in Radians (H-Floating Value) routine returns that angle (in radians) in H-floating-point precision.

Format

MTH$HACOS h-radians ,cosine

Corresponding JSB Entry Points

MTH$HACOS_R8

Returns

None.

Argument

h-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in radians) whose cosine is specified by cosine. The h-radians argument is the address of an H-floating number that is this angle. MTH$HACOS writes the address of the angle into h-radians.

cosine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Description

The angle in radians whose cosine is X is computed as:

Value of Cosine	Value Returned
0	π/2
1	0
-1	π
0 < X < 1	zATAN(zSQRT(1-X ²)/X) , where zATAN and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
-1 < X < 0	zATAN(zSQRT(1-X ²)/X) + π
1 < \|X\|	The error MTH$_INVARGMAT is signaled

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HACOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of cosine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HACOSD

MTH$HACOSD — Arc Cosine of Angle Expressed in Degrees (H-Floating Value). Given the cosine of an angle, the Arc Cosine of Angle Expressed in Degrees (H-Floating Value) routine returns that angle (in degrees) as an H-floating value.

Format

MTH$HACOSD h-degrees ,cosine

Corresponding JSB Entry Points

MTH$HACOSD_R8

Returns

None.

Argument

h-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in degrees) whose cosine is specified by cosine. The h-degrees argument is the address of an H-floating number that is this angle. MTH$HACOSD writes the address of the angle into h-degrees.

cosine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Description

The angle in degrees whose cosine is X is computed as:

Value of Cosine	Angle Returned
0	90
1	0
-1	180
0 < X < 1	zATAND(zSQRT(1-X ²)/X) , where zATAND and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
-1 < X < 0	zATAND(zSQRT(1-X ²)/X) + 180
1 < \|X\|	The error MTH$_INVARGMAT is signaled

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HACOSD routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of cosine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HASIN

MTH$HASIN — Arc Sine in Radians (H-Floating Value). Given the sine of an angle, the Arc Sine in Radians (H-Floating Value) routine returns that angle (in radians) as an H-floating value.

Format

MTH$HASIN h-radians ,sine

Corresponding JSB Entry Points

MTH$HASIN_R8

Returns

None.

Argument

h-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in radians) whose sine is specified by sine. The h-radians argument is the address of an H-floating number that is this angle. MTH$HASIN writes the address of the angle into h-radians.

sine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Description

The angle in radians whose sine is X is computed as:

Value of Sine	Angle Returned
0	0
1	π/2
-1	-π/2
0 < \|X\| < 1	zATAN(X/zSQRT(1-X ²)) , where zATAN and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
1 < \|X\|	The error MTH$_INVARGMAT is signaled

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HASIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of sine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HASIND

MTH$HASIND — Arc Sine in Degrees (H-Floating Value). Given the sine of an angle, the Arc Sine in Degrees (H-Floating Value) routine returns that angle (in degrees) as an H-floating value.

Format

MTH$HASIND h-degrees ,sine

Corresponding JSB Entry Points

MTH$HASIND_R8

Returns

None.

Argument

h-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in degrees) whose sine is specified by sine. The h-degrees argument is the address of an H-floating number that is this angle. MTH$HASIND writes the address of the angle into h-degrees.

sine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Description

The angle in degrees whose sine is X is computed as:

Value of Sine	Value Returned
0	0
1	90
-1	-90
0 < \|X\| < 1	zATAND(X/zSQRT(1-X ²)) , where zATAND and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type
1 < \|X\|	The error MTH$_INVARGMAT is signaled

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HASIND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. The absolute value of sine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HATAN

MTH$HATAN — Arc Tangent in Radians (H-Floating Value). Given the tangent of an angle, the Arc Tangent in Radians (H-Floating Value) routine returns that angle (in radians) as an H-floating value.

Format

MTH$HATAN h-radians ,tangent

Corresponding JSB Entry Points

MTH$HATAN_R8

Returns

None.

Argument

h-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in radians) whose tangent is specified by tangent. The h-radians argument is the address of an H-floating number that is this angle. MTH$HATAN writes the address of the angle into h-radians.

tangent

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The tangent of the angle whose value (in radians) is to be returned. The tangent argument is the address of a floating-point number that is this tangent. For MTH$HATAN, tangent specifies an H-floating number.

Description

In radians, the computation of the arc tangent function is based on the following identities:

arctan(X) = X - X ³/3 + X ⁵/5 - X ⁷/7 + ...
arctan(X) = X + X*Q(X ²),
where Q(Y) = - Y/3 + Y ²/5 - Y ³/7 + ...
arctan(X) = X*P(X ²),
where P(Y) = 1 - Y/3 + Y ²/5 - Y ³/7 + ...
arctan(X) = π/2 - arctan(1/X)
arctan(X) = arctan(A) + arctan((X-A)/(1+A*X))
for any real A

The angle in radians whose tangent is X is computed as:

Value of X	Angle Returned
0 ≤ X ≤ 3/32	X + X * Q(X ²)
3/32 < X ≤ 11	ATAN(A) + V* (P(V ²)) , where A and ATAN(A) are chosen by table lookup and V = (X - A)/(1 + A*X)
11 < X	π/2 - W* (P(W ²)) where W = 1/X
X < 0	-zATAN(\|X\|)

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HATAN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$HATAND

MTH$HATAND — Arc Tangent in Degrees (H-Floating Value). Given the tangent of an angle, the Arc Tangent in Degrees (H-Floating Value) routine returns that angle (in degrees) as an H-floating value.

Format

MTH$HATAND h-degrees ,tangent

Corresponding JSB Entry Points

MTH$HATAND_R8

Returns

None.

Argument

h-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in degrees) whose tangent is specified by tangent. The h-degrees argument is the address of an H-floating number that is this angle. MTH$HATAND writes the address of the angle into h-degrees.

tangent

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The tangent of the angle whose value (in degrees) is to be returned. The tangent argument is the address of a floating-point number that is this tangent. For MTH$HATAND, tangent specifies an H-floating number.

Description

The computation of the arc tangent function is based on the following identities:

arctan(X) = 180/π* (X - X ³/3 + X ⁵/5 - X ⁷/7 + ...)
arctan(X) = 64*X + X*Q(X ²),
where Q(Y) = 180/π*[(1- 64*π/180) - Y/3 +Y ²/5 - Y ³/7 + Y ⁴/9 ...]
arctan(X) = X*P(X ²),
where P(Y) = 180/π*[1 - Y/3 + Y ²/5 - Y ³/7 +Y ⁴/9 ...]
arctan(X) = 90 - arctan>(1/X)
arctan(X) = arctan(A) + arctan((X - A)/(1 + A*X))

The angle in degrees whose tangent is X is computed as:

Tangent	Angle Returned
X ≤ 3/32	64X + XQ(X ²)
3/32 < X ≤ 11	ATAND(A) + VP(V ²) , where A and ATAND(A) are chosen by table lookup and V = (X - A)/(1 + AX)
11 < X	90 - W * (P(W ²)) , where W = 1/X
X < 0	-zATAND(\|X\|)

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HATAND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$HATAN2

MTH$HATAN2 — Arc Tangent in Radians (H-Floating Value) with Two Arguments. Given sine and cosine , the Arc Tangent in Radians (H-Floating Value) with Two Arguments routine returns the angle (in radians) as an H-floating value whose tangent is given by the quotient of sine and cosine (sine /cosine ).

Format

MTH$HATAN2 h-radians ,sine ,cosine

Returns

None.

Argument

h-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in radians) whose tangent is specified by (sine/cosine). The h-radians argument is the address of an H-floating number that is this angle. MTH$HATAN2 writes the address of the angle into h-radians.

sine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Dividend. The sine argument is the address of a floating-point number that is this dividend. For MTH$HATAN2, sine specifies an H-floating number.

cosine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Divisor. The cosine argument is the address of a floating-point number that is this divisor. For MTH$HATAN2, cosine specifies an H-floating number.

Description

The angle in radians whose tangent is Y/X is computed as follows, where f is defined in the description of MTH$zCOSH:

Value of Input Arguments	Angle Returned
X = 0 or Y/X > 2 ^(f+1)	π/2* (signY)
X > 0 and Y/X ≤ 2 ^(f+1)	zATAN(Y/X)
X < 0 and Y/X ≤ 2 ^(f+1)	π* (signY) + zATAN(Y/X)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HATAN2 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. Both cosine and sine are zero. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HATAND2

MTH$HATAND2 — Arc Tangent in Degrees (H-Floating Value) with Two Arguments. Given sine and cosine , the Arc Tangent in Degrees (H-Floating Value) with Two Arguments routine returns the angle (in degrees) whose tangent is given by the quotient of sine and cosine (sine /cosine ).

Format

MTH$HATAND2 h-degrees ,sine ,cosine

Returns

None.

Argument

h-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Angle (in degrees) whose tangent is specified by (sine/cosine). The h-degrees argument is the address of an H-floating number that is this angle. MTH$HATAND2 writes the address of the angle into h-degrees.

sine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Dividend. The sine argument is the address of a floating-point number that is this dividend. For MTH$HATAND2, sine specifies an H-floating number.

cosine

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Divisor. The cosine argument is the address of a floating-point number that is this divisor. For MTH$HATAND2, cosine specifies an H-floating number.

Description

The angle in degrees whose tangent is Y/X is computed below. The value of f is defined in the description of MTH$zCOSH.

Value of Input Arguments	Angle Returned
X = 0 or Y/X > 2 ^(f+1)	90* (signY)
X > 0 and Y/X ≤ 2 ^(f+1)	zATAND(Y/X)
X < 0 and Y/X ≤ 2 ^(f+1)	180 * (signY) + zATAND(Y/X)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HATAND2 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument. Both cosine and sine are zero. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HATANH

MTH$HATANH — Hyperbolic Arc Tangent (H-Floating Value). Given the hyperbolic tangent of an angle, the Hyperbolic Arc Tangent (H-Floating Value) routine returns the hyperbolic arc tangent (as an H-floating value) of that angle.

Format

MTH$HATANH h-atanh ,hyperbolic-tangent

Returns

None.

Argument

h-atanh

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Hyperbolic arc tangent of the hyperbolic tangent specified by hyperbolic-tangent. The h-atanh argument is the address of an H-floating number that is this hyperbolic arc tangent. MTH$HATANH writes the address of the hyperbolic arc tangent into h-atanh.

hyperbolic-tangent

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Hyperbolic tangent of an angle. The hyperbolic-tangent argument is the address of a floating-point number that is this hyperbolic tangent. For MTH$HATANH, hyperbolic-tangent specifies an H-floating number.

Description

The hyperbolic arc tangent function is computed as follows:

Value of X	Value Returned
\|X\| < 1	zATANH(X) = zLOG((X+1)/(X-1))/2
\|X\| ≥ 1	An invalid argument is signaled

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HATANH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_INVARGMAT	Invalid argument: \|X\| = ≥ 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HCOS

MTH$HCOS — Cosine of Angle Expressed in Radians (H-Floating Value). The Cosine of Angle Expressed in Radians (H-Floating Value) routine returns the cosine of a given angle (in radians) as an H-floating value.

Format

MTH$HCOS h-cosine ,angle-in-radians

Corresponding JSB Entry Points

MTH$HCOS_R5

Returns

None.

Argument

h-cosine

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Cosine of the angle specified by angle-in-radians. The h-cosine argument is the address of an H-floating number that is this cosine. MTH$HCOS writes the address of the cosine into h-cosine.

angle-in-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Angle (in radians). The angle-in-radians argument is the address of a floating-point number. For MTH$HCOS, angle-in-radians specifies an H-floating number.

Description

See MTH$xSINCOS for the algorithm used to compute the cosine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HCOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$HCOSD

MTH$HCOSD — Cosine of Angle Expressed in Degrees (H-Floating Value). The Cosine of Angle Expressed in Degrees (H-Floating Value) routine returns the cosine of a given angle (in degrees) as an H-floating value.

Format

MTH$HCOSD h-cosine ,angle-in-degrees

Corresponding JSB Entry Points

MTH$HCOSD_R5

Returns

None.

Argument

h-cosine

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Cosine of the angle specified by angle-in-degrees. The h-cosine argument is the address of an H-floating number that is this cosine. MTH$HCOSD writes this cosine into h-cosine.

angle-in-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Angle (in degrees). The angle-in-degrees argument is the address of a floating-point number. For MTH$HCOSD, angle-in-degrees specifies an H-floating number.

Description

See the MTH$SINCOSD routine for the algorithm used to compute the cosine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HCOSD routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$HCOSH

MTH$HCOSH — Hyperbolic Cosine (H-Floating Value). The Hyperbolic Cosine (H-Floating Value) routine returns the hyperbolic cosine of the input value as an H-floating value.

Format

MTH$HCOSH h-cosh ,floating-point-input-value

Returns

None.

Argument

h-cosh

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Hyperbolic cosine of the input value specified by floating-point-input-value. The h-cosh argument is the address of an H-floating number that is this hyperbolic cosine. MTH$HCOSH writes the address of the hyperbolic cosine into h-cosh.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of this input value. For MTH$HCOSH, floating-point-input-value specifies an H-floating number.

Description

Computation of the hyperbolic cosine depends on the magnitude of the input argument. The range of the function is partitioned using four data-type-dependent constants: a(z), b(z), and c(z). The subscript z indicates the data type. The constants depend on the number of exponent bits (e) and the number of fraction bits (f) associated with the data type (z).

The values of e and f are as follows:

e = 15 f = 113

The values of the constants in terms of e and f are:

Variable	Value
a(z)	2 ^-f/2
b(z)	(f+1)/2*ln(2)
c(z)	2 ^e-1*ln(2)

Based on the above definitions, zCOSH(X) is computed as follows:

Value of X	Value Returned
\|X\| < a(z)	1
a(z) ≤ \|X\| < .25	Computed using a power series expansion in \|X\| ²
.25 ≤ \|X\| < b(z)	(zEXP(\|X\|) + 1/zEXP(\|X\|))/2
b(z) ≤ \|X\| < c(z)	zEXP(\|X\|)/2
c(z) ≤ \|X\|	Overflow occurs

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HCOSH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of floating-point-input-value is greater than about yyy; LIB$SIGNAL copies the reserved operand to the signal mechanism vector. The result is the reserved operand -0.0 unless a condition handler changes the signal mechanism vector. The value of yyy is 11356.523.

MTH$HEXP

MTH$HEXP — Exponential (H-Floating Value). The Exponential (H-Floating Value) routine returns the exponential of the input value as an H-floating value.

Format

MTH$HEXP h-exp ,floating-point-input-value

Corresponding JSB Entry Points

MTH$HEXP_R6

Returns

None.

Argument

h-exp

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Exponential of the input value specified by floating-point-input-value. The h-exp argument is the address of an H-floating number that is this exponential. MTH$HEXP writes the address of the exponential into h-exp.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number. For MTH$HEXP, floating-point-input-value specifies an H-floating number.

Description

The exponential of x is computed as:

Value of x	Value Returned
x > c(z)	Overflow occurs
x ≤ -c(z)	0
\|x\| < 2 ^-(f+1)	1
Otherwise	2 ^Y * 2 ^U * 2 ^W

where: Y = INTEGER(x*ln2(E)) V = FRAC(x*ln2(E)) * 16 U = INTEGER(V)/16 W = FRAC(V)/16 2^W = polynomial approximation of degree 14 for z = H.

See also MTH$HCOS for definitions of f and c(z).

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HEXP routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: floating-point-input-value is greater than yyy; LIB$SIGNAL copies the reserved operand to the signal mechanism vector. The result is the reserved operand -0.0 unless a condition handler changes the signal mechanism vector. The value of yyy is approximately 11355.830 for MTH$HEXP.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library: floating-point-input-value is less than or equal to yyy and the caller (CALL or JSB) has set hardware floating-point underflow enable. The result is set to 0.0. If the caller has not enabled floating-point underflow (the default), a result of 0.0 is returned but no error is signaled. The value of yyy is approximately --11356.523 for MTH$HEXP.

MTH$HLOG

MTH$HLOG — Natural Logarithm (H-Floating Value). The Natural Logarithm (H-Floating Value) routine returns the natural (base e) logarithm of the input argument as an H-floating value.

Format

MTH$HLOG h-natlog ,floating-point-input-value

Corresponding JSB Entry Points

MTH$HLOG_R8

Returns

None.

Argument

h-natlog

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Natural logarithm of floating-point-input-value. The h-natlog argument is the address of an H-floating number that is this natural logarithm. MTH$HLOG writes the address of this natural logarithm into h-natlog.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that is this value. For MTH$HLOG, floating-point-input-value specifies an H-floating number.

Description

Computation of the natural logarithm routine is based on the following:

ln(X*Y) = ln(X) + ln(Y)
- ln(1+X) = X - X²/2 + X³/3 - X⁴/4 ...
- for |X| < 1
- ln(X) = ln(A) + 2* (V + V³/3 + V⁵/5 + V⁷/7 ...)
- where V = (X-A)/(X+A), A > 0,
- and p(y) = 2 * (1 + y/3 + y²/5 ...)
For x = 2ⁿ*f, where n is an integer and f is in the interval of 0.5 to 1, define the following quantities:
If n ≥ 1, then N = n-1 and F = 2f
If n ≤ 0, then N = n and F = f
From (1) it follows that:
ln(X) = N*ln(2) + ln(F)

Based on the previous relationships, zLOG is computed as follows:

- If |F-1| < 2^-5,
- zLOG(X) = N*zLOG(2) + W + W*p(W),
- where W = F-1.
- Otherwise,
- zLOG(X) = N*zLOG(2) + zLOG(A) + V*p(V²),
- where V = (F-A)/(F+A) and A and zLOG(A)
- are obtained by table lookup.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HLOG routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_LOGZERNEG	Logarithm of zero or negative value. Argument floating-point-input-value is less than or equal to 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HLOG2

MTH$HLOG2 — Base 2 Logarithm (H-Floating Value). The Base 2 Logarithm (H-Floating Value) routine returns the base 2 logarithm of the input value specified by floating-point-input-value as an H-floating value.

Format

MTH$HLOG2 h-log2 ,floating-point-input-value

Returns

None.

Argument

h-log2

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Base 2 logarithm of floating-point-input-value. The h-log2 argument is the address of an H-floating number that is this base 2 logarithm. MTH$HLOG2 writes the address of this logarithm into h-log2.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that is this input value. For MTH$HLOG2, floating-point-input-value specifies an H-floating number.

Description

The base 2 logarithm function is computed as follows:

zLOG2(X) = zLOG2(E) * zLOG(X)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HLOG2 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_LOGZERNEG	Logarithm of zero or negative value. Argument floating-point-input-value is less than or equal to 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HLOG10

MTH$HLOG10 — Common Logarithm (H-Floating Value). The Common Logarithm (H-Floating Value) routine returns the common (base 10) logarithm of the input argument as an H-floating value.

Format

MTH$HLOG10 h-log10 ,floating-point-input-value

Corresponding JSB Entry Points

MTH$HLOG10_R8

Returns

None.

Argument

h-log10

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Common logarithm of the input value specified by floating-point-input-value. The h-log10 argument is the address of an H-floating number that is this common logarithm. MTH$HLOG10 writes the address of the common logarithm into h-log10.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number. For MTH$HLOG10, floating-point-input-value specifies an H-floating number.

Description

The common logarithm function is computed as follows:

zLOG10(X) = zLOG10(E) * zLOG(X)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HLOG10 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_LOGZERNEG	Logarithm of zero or negative value. Argument floating-point-input-value is less than or equal to 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HSIN

MTH$HSIN — Sine of Angle Expressed in Radians (H-Floating Value). The Sine of Angle Expressed in Radians (H-Floating Value) routine returns the sine of a given angle (in radians) as an H-floating value.

Format

MTH$HSIN h-sine ,angle-in-radians

Corresponding JSB Entry Points

MTH$HSIN_R5

Returns

None.

Argument

h-sine

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

The sine of the angle specified by angle-in-radians. The h-sine argument is the address of an H-floating number that is this sine. MTH$HSIN writes the address of the sine into h-sine.

angle-in-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Angle (in radians). The angle-in-radians argument is the address of a floating-point number that is this angle. For MTH$HSIN, angle-in-radians specifies an H-floating number.

Description

See MTH$xSINCOS for the algorithm used to compute this sine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HSIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$HSIND

MTH$HSIND — Sine of Angle Expressed in Degrees (H-Floating Value). The Sine of Angle Expressed in Degrees (H-Floating Value) routine returns the sine of a given angle (in degrees) as an H-floating value.

Format

MTH$HSIND h-sine ,angle-in-degrees

Corresponding JSB Entry Points

MTH$HSIND_R5

Returns

None.

Argument

h-sine

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Sine of the angle specified by angle-in-degrees. MTH$HSIND writes into h-sine the address of an H-floating number that is this sine.

angle-in-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Angle (in degrees). The angle-in-degrees argument is the address of an H-floating number that is this angle.

Description

See MTH$xSINCOSD for the algorithm used to compute the sine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HSIND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library. The absolute value of the input angle is less than 180/π*2 ^-m (where m = 16,384 for H-floating).

MTH$HSINH

MTH$HSINH — Hyperbolic Sine (H-Floating Value). The Hyperbolic Sine (H-Floating Value) routine returns the hyperbolic sine of the input value specified by floating-point-input-value as an H-floating value.

Format

MTH$HSINH h-sinh ,floating-point-input-value

Returns

None.

Argument

h-sinh

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Hyperbolic sine of the input value specified by floating-point-input-value. The h-sinh argument is the address of an H-floating number that is this hyperbolic sine. MTH$HSINH writes the address of the hyperbolic sine into h-sinh.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that is this value. For MTH$HSINH, floating-point-input-value specifies an H-floating number.

Description

Computation of the hyperbolic sine function depends on the magnitude of the input argument. The range of the function is partitioned using three data type dependent constants: a(z), b(z), and c(z). The subscript z indicates the data type. The constants depend on the number of exponent bits (e) and the number of fraction bits (f) associated with the data type (z).

The values of e and f are as follows:

e = 15

f = 113

The values of the constants in terms of e and f are:

Variable	Value
a(z)	2 ^(-f/2)
b(z)	(f+1)/2*ln(2)
c(z)	2 ^e-1*ln(2)

Based on the above definitions, zSINH(X) is computed as follows:

Value of X	Value Returned
\|X\| < a(z)	X
a(z) ≤ \|X\| < 1.0	zSINH(X) is computed using a power series expansion in \|X\| ²
1.0 ≤ \|X\| < b(z)	(zEXP(X) - zEXP(-X))/2
b(z) ≤ \|X\| < c(z)	SIGN(X)*zEXP(\|X\|)/2
c(z) ≤ \|X\|	Overflow occurs

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HSINH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library: the absolute value of floating-point-input-value is greater than yyy. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1. The value of yyy is approximately 11356.523.

MTH$HSQRT

MTH$HSQRT — Square Root (H-Floating Value). The Square Root (H-Floating Value) routine returns the square root of the input value floating-point-input-value as an H-floating value.

Format

MTH$HSQRT h-sqrt ,floating-point-input-value

Corresponding JSB Entry Points

MTH$HSQRT_R8

Returns

None.

Argument

h-sqrt

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Square root of the input value specified by floating-point-input-value. The h-sqrt argument is the address of an H-floating number that is this square root. MTH$HSQRT writes the address of the square root into h-sqrt.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

Input value. The floating-point-input-value argument is the address of a floating-point number that contains this input value. For MTH$HSQRT, floating-point-input-value specifies an H-floating number.

Description

The square root of X is computed as follows:

If X < 0 , an error is signaled.

Let X = 2 ^K * F

where:

K is the exponential part of the floating-point data

F is the fractional part of the floating-point data

If K is even:

X = 2 ^(2*P) * F,zSQRT(X) = 2 ^P * zSQRT(F),1/2 ≤ F < 1 , where P = K/2

If K is odd:

X = 2 ^(2*P+1) * F = 2 ^(2*P+2) * (F/2) ,zSQRT(X) = 2 ^(P+1) * zSQRT(F/2),1/4 ≤ F/2 < 1/2 , where p = (K-1)/2

Let F' = A * F + B, when K is even:

A = 0.95F6198 (hex)

B = 0.6BA5918 (hex)

Let F' = A* (F/2) + B, when K is odd:

A = 0.D413CCC (hex)

B = 0.4C1E248 (hex)

Let K' = P, when K is even

Let K' = P+1, when K is odd

Let Y[0] = 2^K' * F' be a straight line approximation within the given interval using coefficients A and B, which minimize the absolute error at the midpoint and endpoint.

Starting with Y[0], n Newton-Raphson iterations are performed:

Y[n+1] = 1/2 * (Y[n] + X/Y[n])

where n = 5 for H-floating.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HSQRT routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_SQUROONEG	Square root of negative number. Argument floating-point-input-value is less than 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$HTAN

MTH$HTAN — Tangent of Angle Expressed in Radians (H-Floating Value). The Tangent of Angle Expressed in Radians (H-Floating Value) routine returns the tangent of a given angle (in radians) as an H-floating value.

Format

MTH$HTAN h-tan ,angle-in-radians

Corresponding JSB Entry Points

MTH$HTAN_R5

Returns

None.

Argument

h-tan

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Tangent of the angle specified by angle-in-radians. The h-tan argument is the address of an H-floating number that is this tangent. MTH$HTAN writes the address of the tangent into h-tan.

angle-in-radians

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input angle (in radians). The angle-in-radians argument is the address of a floating-point number that is this angle. For MTH$HTAN, angle-in-radians specifies an H-floating number.

Description

When the input argument is expressed in radians, the tangent function is computed as follows:

If |X| < 2^(-f/2), then zTAN(X) = X (see the section on MTH$zCOSH for the definition of f)
Otherwise, call MTH$zSINCOS to obtain zSIN(X) and zCOS(X); then
- If zCOS(X) = 0 , signal overflow
- Otherwise, zTAN(X) = zSIN(X)/zCOS(X)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HTAN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library.

MTH$HTAND

MTH$HTAND — Tangent of Angle Expressed in Degrees (H-Floating Value). The Tangent of Angle Expressed in Degrees (H-Floating Value) routine returns the tangent of a given angle (in degrees) as an H-floating value.

Format

MTH$HTAND h-tan ,angle-in-degrees

Corresponding JSB Entry Points

MTH$HTAND_R5

Returns

None.

Argument

h-tan

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Tangent of the angle specified by angle-in-degrees. The h-tan argument is the address of an H-floating number that is this tangent. MTH$HTAND writes the address of the tangent into h-tan.

angle-in-degrees

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input angle (in degrees). The angle-in-degrees argument is the address of a floating-point number that is this angle. For MTH$HTAND, angle-in-degrees specifies an H-floating number.

Description

When the input argument is expressed in degrees, the tangent function is computed as follows:

If |X| < (180/π)*2^(-2/(e-1)) and underflow signaling is enabled, underflow is signaled (see the section on MTH$zCOSH for the definition of e).
Otherwise, if |X| < (180/π)*2^(-f/2)
, then zTAND(X) = (π/180)*X. See the description of MTH$zCOSH for the definition of f.
Otherwise, call MTH$zSINCOSD to obtain zSIND(X) and zCOSD(X).
- Then, if zCOSD(X) = 0 , signal overflow
- Else, zTAND(X) = zSIND(X)/zCOSD(X)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$HTAND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library.

MTH$HTANH

MTH$HTANH — Compute the Hyperbolic Tangent (H-Floating Value). The Compute the Hyperbolic Tangent (H-Floating Value) routine returns the hyperbolic tangent of the input value as an H-floating value.

Format

MTH$HTANH h-tanh ,floating-point-input-value

Returns

None.

Argument

h-tanh

OpenVMS usage:	floating_point
type:	H_floating
access:	write only
mechanism:	by reference

Hyperbolic tangent of the value specified by floating-point-input-value. The h-tanh argument is the address of an H-floating number that is this hyperbolic tangent. MTH$HTANH writes the address of the hyperbolic tangent into h-tanh.

floating-point-input-value

OpenVMS usage:	floating_point
type:	H_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of an H-floating number that contains this input value.

Description

For MTH$HTANH, the hyperbolic tangent of X is computed using a value of 56 for g and a value of 40 for h. The hyperbolic tangent of X is computed as follows:

Value of x	Hyperbolic Tangent Returned
\|X\| ≤ 2 ^-g	X
2 ^-g < \|X\| ≤ 0.25	zSINH(X)/zCOSH(X)
0.25 < \|X\| < h	(zEXP(2X) - 1)/(zEXP(2X) + 1)
h ≤ \|X\|	sign(X) * 1

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HTANH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xIMAG

MTH$xIMAG — Imaginary Part of a Complex Number. The Imaginary Part of a Complex Number routine returns the imaginary part of a complex number.

Format

MTH$AIMAG complex-number

MTH$DIMAG complex-number

MTH$GIMAG complex-number

Each of the above formats corresponds to one of the floating-point complex types.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Imaginary part of the input complex-number. MTH$AIMAG returns an F-floating number. MTH$DIMAG returns a D-floating number. MTH$GIMAG returns a G-floating number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex, D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

The input complex number. The complex-number argument is the address of this floating-point complex number. For MTH$AIMAG, complex-number specifies an F-floating number. For MTH$DIMAG, complex-number specifies a D-floating number. For MTH$GIMAG, complex-number specifies a G-floating number.

Description

The MTH$xIMAG routines return the imaginary part of a complex number.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xIMAG routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

C+ 
C    This Fortran example forms the imaginary part of 
C    a G-floating complex number using MTH$GIMAG 
C    and the Fortran random number generator 
C    RAN. 
C 
C    Declare Z as a complex value and MTH$GIMAG as 
C    a REAL*8 value. MTH$GIMAG will return the imaginary 
C    part of Z:   Z_NEW = MTH$GIMAG(Z). 
C- 
 
        COMPLEX*16 Z 
        COMPLEX*16 DCMPLX 
        REAL*8 R,I,MTH$GIMAG 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the 
C    Fortran generic CMPLX. 
C- 
 
        R = RAN(M) 
        I = RAN(M) 
        Z = DCMPLX(R,I) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and 
C    imaginary part "i". 
C- 
 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' It has imaginary part',MTH$GIMAG(Z) 
        END

This Fortran example demonstrates a procedure call to MTH$GIMAG. Because this example uses G-floating numbers, it must be compiled with the statement "FORTRAN/G filename".

The output generated by this program is as follows:

The complex number z is (0.8535407185554504,0.2043401598930359) 
It has imaginary part  0.2043401598930359

MTH$xLOG

MTH$xLOG — Natural Logarithm. The Natural Logarithm routine returns the natural (base e) logarithm of the input argument.

Format

MTH$ALOG floating-point-input-value

MTH$DLOG floating-point-input-value

MTH$GLOG floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ALOG_R5

MTH$DLOG_R8

MTH$GLOG_R8

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The natural logarithm of floating-point-input-value. MTH$ALOG returns an F-floating number. MTH$DLOG returns a D-floating number. MTH$GLOG returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that is this value. For MTH$ALOG, floating-point-input-value specifies an F-floating number. For MTH$DLOG, floating-point-input-value specifies a D-floating number. For MTH$GLOG, floating-point-input-value specifies a G-floating number.

Description

Computation of the natural logarithm routine is based on the following:

ln(X*Y) = ln(X) + ln(Y)
ln(1+X) = X - X²/2 + X³/3 - X⁴/4 ...
for |X| < 1
ln(X) = ln(A) + 2* (V + V³/3 + V⁵/5 + V⁷/7 ...)
=ln(A) + V*p(V²), where V = (X-A)/(X+A),
A > 0, and p(y) = 2 * (1 + y/3 + y²/5 ...)
For x = 2ⁿ*f , where n is an integer and f is in the interval of 0.5 to 1, define the following quantities:
If n ≥ 1, then N = n-1 and F = 2f
If n ≤ 0, then N = n and F = f
From (1) above it follows that:
ln(X) = N*ln(2) + ln(F)

Based on the above relationships, zLOG is computed as follows:

If |F-1| < 2^-5, zLOG(X) = N*zLOG(2) + W + W*p(W),
where W = F-1.
Otherwise, zLOG(X) = N*zLOG(2) + zLOG(A) + V*p(V²),
where V = (F-A)/(F+A) and A and zLOG(A)
are obtained by table lookup.

See MTH$HLOG for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xLOG routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_LOGZERNEG	Logarithm of zero or negative value. Argument floating-point-input-value is less than or equal to 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xLOG2

MTH$xLOG2 — Base 2 Logarithm. The Base 2 Logarithm routine returns the base 2 logarithm of the input value specified by floating-point-input-value.

Format

MTH$ALOG2 floating-point-input-value

MTH$DLOG2 floating-point-input-value

MTH$GLOG2 floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The base 2 logarithm of floating-point-input-value. MTH$ALOG2 returns an F-floating number. MTH$DLOG2 returns a D-floating number. MTH$GLOG2 returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that is this input value. For MTH$ALOG2, floating-point-input-value specifies an F-floating number. For MTH$DLOG2, floating-point-input-value specifies a D-floating number. For MTH$GLOG2, floating-point-input-value specifies a G-floating number.

Description

The base 2 logarithm function is computed as follows:

zLOG2(X) = zLOG2(E) * zLOG(X)

See MTH$HLOG2 for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xLOG2 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_LOGZERNEG	Logarithm of zero or negative value. Argument floating-point-input-value is less than or equal to 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xLOG10

MTH$xLOG10 — Common Logarithm. The Common Logarithm routine returns the common (base 10) logarithm of the input argument.

Format

MTH$ALOG10 floating-point-input-value

MTH$DLOG10 floating-point-input-value

MTH$GLOG10 floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$ALOG10_R5

MTH$DLOG10_R8

MTH$GLOG10_R8

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The common logarithm of floating-point-input-value. MTH$ALOG10 returns an F-floating number. MTH$DLOG10 returns a D-floating number. MTH$GLOG10 returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number. For MTH$ALOG10, floating-point-input-value specifies an F-floating number. For MTH$DLOG10, floating-point-input-value specifies a D-floating number. For MTH$GLOG10, floating-point-input-value specifies a G-floating number.

Description

The common logarithm function is computed as follows:

zLOG10(X) = zLOG10(E) * zLOG(X)

See MTH$HLOG10 for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xLOG10 routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_LOGZERNEG	Logarithm of zero or negative value. Argument floating-point-input-value is less than or equal to 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$RANDOM

MTH$RANDOM — Random Number Generator, Uniformly Distributed. The Random Number Generator, Uniformly Distributed routine is a general random number generator.

Format

MTH$RANDOM seed

Returns

OpenVMS usage:	floating_point
type:	F_floating
access:	write only
mechanism:	by value

MTH$RANDOM returns an F-floating random number.

Argument

seed

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	modify
mechanism:	by reference

The integer seed, a 32-bit number whose high-order 24 bits are converted by MTH$RANDOM to an F-floating random number. The seed argument is the address of an unsigned longword that contains this integer seed. The seed is modified by each call to MTH$RANDOM.

Description

This routine must be called again to obtain the next pseudorandom number. The seed is updated automatically.

The result is a floating-point number that is uniformly distributed between 0.0 inclusively and 1.0 exclusively.

There are no restrictions on the seed, although it should be initialized to different values on separate runs in order to obtain different random sequences. MTH$RANDOM uses the following method to update the seed passed as the argument:

SEED = (69069 * SEED + 1) (modulo 2³²)

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$RANDOM routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

RAND:   PROCEDURE OPTIONS (MAIN); 
DECLARE FOR$SECNDS ENTRY (FLOAT BINARY (24)) 
                RETURNS (FLOAT BINARY (24)); 
DECLARE MTH$RANDOM ENTRY (FIXED BINARY (31)) 
                RETURNS (FLOAT BINARY (24)); 
DECLARE TIME FLOAT BINARY (24); 
DECLARE SEED FIXED BINARY (31); 
DECLARE I FIXED BINARY (7); 
DECLARE RESULT FIXED DECIMAL (2); 
        /* Get floating random time value       */ 
TIME = FOR$SECNDS (0E0); 
        /* Convert to fixed                     */ 
SEED = TIME; 
        /* Generate 100 random numbers between 1 and 10 */ 
DO I = 1 TO 100; 
        RESULT = 1 + FIXED ( (10E0 * MTH$RANDOM (SEED) ),31 ); 
        PUT LIST (RESULT); 
        END; 
END RAND;

This PL/I program demonstrates the use of MTH$RANDOM. The value returned by FOR$SECNDS is used as the seed for the random-number generator to ensure a different sequence each time the program is run. The random value returned is scaled so as to represent values between 1 and 10.

Because this program generates random numbers, the output generated will be different each time the program is executed. One example of the outut generated by this program is as follows:

7    4    6    5    9   10    5    5    3    8    8    1   3    1    3    2 
4    4    2    4    4    8    3    8    9    1    7    1   8    6    9   10 
1   10   10    6    7    3    2    2    1    2    6    6   3    9    5    8 
6    2    3    6   10    8    5    5    4    2    8    5   9    6    4    2 
8    5    4    9    8    7    6    6    8   10    9    5   9    4    5    7 
1    2    2    3    6    5    2    3    4    4    8    9   2    8    5    5 
3    8    1    5

MTH$xREAL

MTH$xREAL — Real Part of a Complex Number. The Real Part of a Complex Number routine returns the real part of a complex number.

Format

MTH$REAL complex-number

MTH$DREAL complex-number

MTH$GREAL complex-number

Each of the above formats accepts one of the floating-point complex types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Real part of the complex number. MTH$REAL returns an F-floating number. MTH$DREAL returns a D-floating number. MTH$GREAL returns a G-floating number.

Argument

complex-number

OpenVMS usage:	complex_number
type:	F_floating complex, D_floating complex, G_floating complex
access:	read only
mechanism:	by reference

The complex number whose real part is returned by MTH$xREAL. The complex-number argument is the address of this floating-point complex number. For MTH$REAL, complex-number is an F-floating complex number. For MTH$DREAL, complex-number is a D-floating complex number. For MTH$GREAL, complex-number is a G-floating complex number.

Description

The MTH$xREAL routines return the real part of a complex number.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xREAL routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

Example

C+ 
C    This Fortran example forms the real 
C    part of an F-floating complex number using 
C    MTH$REAL and the Fortran random number 
C    generator RAN. 
C 
C    Declare Z as a complex value and MTH$REAL as a 
C    REAL*4 value.  MTH$REAL will return the real 
C    part of Z:   Z_NEW = MTH$REAL(Z). 
C- 
 
        COMPLEX Z 
        COMPLEX CMPLX 
        REAL*4 MTH$REAL 
        INTEGER M 
        M = 1234567 
 
C+ 
C    Generate a random complex number with the Fortran 
C    generic CMPLX. 
C- 
 
        Z = CMPLX(RAN(M),RAN(M)) 
 
C+ 
C    Z is a complex number (r,i) with real part "r" and imaginary 
C    part "i". 
C- 
 
        TYPE *, ' The complex number z is',z 
        TYPE *, ' It has real part',MTH$REAL(Z) 
        END

This Fortran example demonstrates the use of MTH$REAL. The output of this program is as follows:

The complex number z is (0.8535407,0.2043402) 
It has real part  0.8535407

MTH$xSIN

MTH$xSIN — Sine of Angle Expressed in Radians. The Sine of Angle Expressed in Radians routine returns the sine of a given angle (in radians).

Format

MTH$SIN angle-in-radians

MTH$DSIN angle-in-radians

MTH$GSIN angle-in-radians

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$SIN_R4

MTH$DSIN_R7

MTH$GSIN_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Sine of the angle specified by angle-in-radians. MTH$SIN returns an F-floating number. MTH$DSIN returns a D-floating number. MTH$GSIN returns a G-floating number.

Argument

angle-in-radians

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Angle (in radians). The angle-in-radians argument is the address of a floating-point number that is this angle. For MTH$SIN, angle-in-radians specifies an F-floating number. For MTH$DSIN, angle-in-radians specifies a D-floating number. For MTH$GSIN, angle-in-radians specifies a G-floating number.

Description

See MTH$xSINCOS for the algorithm used to compute this sine.

See MTH$HSIN for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xSIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xSINCOS

MTH$xSINCOS — Sine and Cosine of Angle Expressed in Radians. The Sine and Cosine of Angle Expressed in Radians routine returns the sine and cosine of a given angle (in radians).

Format

MTH$SINCOS angle-in-radians ,sine ,cosine

MTH$DSINCOS angle-in-radians ,sine ,cosine

MTH$GSINCOS angle-in-radians ,sine ,cosine

MTH$HSINCOS angle-in-radians ,sine ,cosine

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$SINCOS_R5

MTH$DSINCOS_R7

MTH$GSINCOS_R7

MTH$HSINCOS_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

MTH$SINCOS, MTH$DSINCOS, MTH$GSINCOS, and MTH$HSINCOS return the sine and cosine of the input angle by reference in the sine and cosine arguments.

Argument

angle-in-radians

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating, H_floating
access:	read only
mechanism:	by reference

Angle (in radians) whose sine and cosine are to be returned. The angle-in-radians argument is the address of a floating-point number that is this angle. For MTH$SINCOS, angle-in-radians is an F-floating number. For MTH$DSINCOS, angle-in-radians is a D-floating number. For MTH$GSINCOS, angle-in-radians is a G-floating number. For MTH$HSINCOS, angle-in-radians is an H-floating number.

sine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating, H_floating
access:	write only
mechanism:	by reference

Sine of the angle specified by angle-in-radians. The sine argument is the address of a floating-point number. MTH$SINCOS writes an F-floating number into sine. MTH$DSINCOS writes a D-floating number into sine. MTH$GSINCOS writes a G-floating number into sine. MTH$HSINCOS writes an H-floating number into sine.

cosine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating, H_floating
access:	write only
mechanism:	by reference

Cosine of the angle specified by angle-in-radians. The cosine argument is the address of a floating-point number. MTH$SINCOS writes an F-floating number into cosine. MTH$DSINCOS writes a D-floating number into cosine. MTH$GSINCOS writes a G-floating number into cosine. MTH$HSINCOS writes an H-floating number into cosine.

Description

All routines with JSB entry points accept a single argument in R0:Rm, where m, which is defined below, is dependent on the data type.

Data Type	m
F_floating	0
D_floating	1
G_floating	1
H_floating	3

In general, Run-Time Library routines with JSB entry points return one value in R0:Rm. The MTHxSINCOS routine returns two values, however. The sine of angle-in-radians is returned in R0:Rm and the cosine of angle-in-radians is returned in (R<m+1>:R<2*m+1>).

In radians, the computation of zSIN(X) and zCOS(X) is based on the following polynomial expansions:

- sin(X) = X - X³/(3!) + X⁵/(5!) - X⁷/(7!) ...
- =X + X*P(X²), where
- P(y) = y/(3!) + y²/(5!) + y³/(7!) ...
- cos(X) = 1 - X²/(2!) + x⁴/(4!) -X⁶/(6!) ...
- =Q(X²), where
- Q(y) = (1 - y/(2!) + y²/(4!) + y³/(6!) ...)

If |X| < 2^(-f/2),
then zSIN(X) = X and zCOS(X) = 1
(see the section on MTH$zCOSH for
the definition of f)
If 2^-f/2 ≤ |X| < π/4,
then zSIN(X) = X + P(X²)
and zCOS(X) = Q(X²)
If π/4 ≤ |X| and X > 0,
1. Let J = INT(X/(π/4))
  and I = J modulo 8
2. If J is even, let Y = X - J* (π/4)
  otherwise, let Y = (J+1)* (π/4) - X
  With the above definitions, the following table relates zSIN(X) and zCOS(X) to zSIN(Y) and zCOS(Y):
  Value of I zSIN(X) zCOS(X)
  0 zSIN(Y) zCOS(Y)
  1 zCOS(Y) zSIN(Y)
  2 zCOS(Y) -zSIN(Y)
  3 zSIN(Y) -zCOS(Y)
  4 -zSIN(Y) -zCOS(Y)
  5 -zCOS(Y) -zSIN(Y)
  6 -zCOS(Y) zSIN(Y)
  7 -zSIN(Y) zCOS(Y)
3. zSIN(Y) and zCOS(Y) are computed as follows:
  zSIN(Y) = Y + P(Y²),
  and zCOS(Y) = Q(Y²)
If π/4 ≤ |X| and X < 0,
then zSIN(X) = -zSIN(|X|)
and zCOS(X) = zCOS(|X|)

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xSINCOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$xSINCOSD

MTH$xSINCOSD — Sine and Cosine of Angle Expressed in Degrees. The Sine and Cosine of Angle Expressed in Degrees routine returns the sine and cosine of a given angle (in degrees).

Format

MTH$SINCOSD angle-in-degrees ,sine ,cosine

MTH$DSINCOSD angle-in-degrees ,sine ,cosine

MTH$GSINCOSD angle-in-degrees ,sine ,cosine

MTH$HSINCOSD angle-in-degrees ,sine ,cosine

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$SINCOSD_R5

MTH$DSINCOSD_R7

MTH$GSINCOSD_R7

MTH$HSINCOSD_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

MTH$SINCOSD, MTH$DSINCOSD, MTH$GSINCOSD, and MTH$HSINCOSD return the sine and cosine of the input angle by reference in the sine and cosine arguments.

Argument

angle-in-degrees

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating, H_floating
access:	read only
mechanism:	by reference

Angle (in degrees) whose sine and cosine are returned by MTH$xSINCOSD. The angle-in-degrees argument is the address of a floating-point number that is this angle. For MTH$SINCOSD, angle-in-degrees is an F-floating number. For MTH$DSINCOSD, angle-in-degrees is a D-floating number. For MTH$GSINCOSD, angle-in-degrees is a G-floating number. For MTH$HSINCOSD, angle-in-degrees is an H-floating number.

sine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating, H_floating
access:	write only
mechanism:	by reference

Sine of the angle specified by angle-in-degrees. The sine argument is the address of a floating-point number. MTH$SINCOSD writes an F-floating number into sine. MTH$DSINCOSD writes a D-floating number into sine. MTH$GSINCOSD writes a G-floating number into sine. MTH$HSINCOSD writes an H-floating number into sine.

cosine

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating, H_floating
access:	write only
mechanism:	by reference

Cosine of the angle specified by angle-in-degrees. The cosine argument is the address of a floating-point number. MTH$SINCOSD writes an F-floating number into cosine. MTH$DSINCOSD writes a D-floating number into cosine. MTH$GSINCOSD writes a G-floating number into cosine. MTH$HSINCOSD writes an H-floating number into cosine.

Description

All routines with JSB entry points accept a single argument in R0:Rm, where m, which is defined below, is dependent on the data type.

Data Type	m
F_floating	0
D_floating	1
G_floating	1
H_floating	3

In general, Run-Time Library routines with JSB entry points return one value in R0:Rm. The MTH$xSINCOSD routine returns two values, however. The sine of angle-in-degrees is returned in R0:Rm and the cosine of angle-in-degrees is returned in (R<m+1>:R<2*m+1>).

In degrees, the computation of zSIND(X) and zCOSD(X) is based on the following polynomial expansions:

- SIND(X) = (C*X) - (C*X)³/(3!) +
- (C*X)⁵/(5!) - (C*X)⁷/(7!) ...
- = X/2⁶ + X*P(X²), where
- P(y) = -y/(3!) + y²/(5!) - y³/(7!) ...
- COSD(X) = 1 - (C*X)²/(2!) +
- (C*X)⁴/(4!) - (C*X)⁶/(6!) ...
- =Q(X²), where
- Q(y) = 1 - y/(2!) + y²/(4!) - y³/(6!) ...
- and C = π/180

If |X| <(180/π)*2^{-2^e-1} and underflow signaling is enabled,
underflow is signaled for zSIND(X) and zSINCOSD(X).
(See MTH$zCOSH for the definition of e.)
otherwise:
If |X| < (180/π)*2^(-f/2),
then zSIND(X)= (π/180)*X and zCOSD(X) = 1.
(See MTH$zCOSH for the definition of f.)
If (180/π)*2^(-f/2) ≤ |X| < 45
then zSIND(X) = X/2⁶ + P(X²)
and zCOSD(X) = Q(X²)
If 45 ≤ |X| and X > 0,
1. Let J = INT(X/(45)) and
  I = J modulo 8
2. If J is even, let Y = X - J*45 ;
  otherwise, let Y = (J+1)*45 - X.
  With the above definitions, the following table relates
  zSIND(X) and zCOSD(X) to zSIND(Y) and zCOSD(Y):
  Value of I zSIND(X) zCOSD(X)
  0 zSIND(Y) zCOSD(Y)
  1 zCOSD(Y) zSIND(Y)
  2 zCOSD(Y) -zSIND(Y)
  3 zSIND(Y) -zCOSD(Y)
  4 -zSIND(Y) -zCOSD(Y)
  5 -zCOSD(Y) -zSIND(Y)
  6 -zCOSD(Y) zSIND(Y)
  7 -zSIND(Y) zCOSD(Y)
3. zSIND(Y) and zCOSD(Y) are computed as follows:
  zSIND(Y) = Y/2⁶ + P(Y²)
  zCOSD(Y) = Q(Y²)
4. If 45 ≤ |X| and X < 0,
  then zSIND(X) = -zSIND(|X|)
  and zCOSD(X) = zCOSD(|X|)

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xSINCOSD routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library. The absolute value of the input angle is less than 180/π*2 ^-m (where m = 128 for F-floating and D-floating, 1,024 for G-floating, and 16,384 for H-floating).

MTH$xSIND

MTH$xSIND — Sine of Angle Expressed in Degrees. The Sine of Angle Expressed in Degrees routine returns the sine of a given angle (in degrees).

Format

MTH$SIND angle-in-degrees

MTH$DSIND angle-in-degrees

MTH$GSIND angle-in-degrees

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$SIND_R4

MTH$DSIND_R7

MTH$GSIND_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The sine of the angle. MTH$SIND returns an F-floating number. MTH$DSIND returns a D-floating number. MTH$GSIND returns a G-floating number.

Argument

angle-in-degrees

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Angle (in degrees). The angle-in-degrees argument is the address of a floating-point number that is this angle. For MTH$SIND, angle-in-degrees specifies an F-floating number. For MTH$DSIND, angle-in-degrees specifies a D-floating number. For MTH$GSIND, angle-in-degrees specifies a G-floating number.

Description

See MTH$xSINCOSD for the algorithm that is used to compute the sine.

See MTH$HSIND for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xSIND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library. The absolute value of the input angle is less than 180/π*2 ^-m (where m = 128 for F-floating and D-floating, and 1,024 for G-floating).

MTH$xSINH

MTH$xSINH — Hyperbolic Sine. The Hyperbolic Sine routine returns the hyperbolic sine of the input value specified by floating-point-input-value.

Format

MTH$SINH floating-point-input-value

MTH$DSINH floating-point-input-value

MTH$GSINH floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The hyperbolic sine of floating-point-input-value. MTH$SINH returns an F-floating number. MTH$DSINH returns a D-floating number. MTH$GSINH returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that is this value. For MTH$SINH, floating-point-input-value specifies an F-floating number. For MTH$DSINH, floating-point-input-value specifies a D-floating number. For MTH$GSINH, floating-point-input-value specifies a G-floating number.

Description

Computation of the hyperbolic sine function depends on the magnitude of the input argument. The range of the function is partitioned using four data type dependent constants: a(z), b(z), and c(z). The subscript z indicates the data type. The constants depend on the number of exponent bits (e) and the number of fraction bits (f) associated with the data type (z).

The values of e and f are:

z	e	f
F	8	24
D	8	56
G	11	53

The values of the constants in terms of e and f are:

Variable	Value
a(z)	2 ^(-f/2)
b(z)	CEILING[ (f+1)/2*ln(2) ]
c(z)	(2 ^(e-1)*ln(2))

Based on the above definitions, zSINH(X) is computed as follows:

Value of X	Value Returned
\|X\| < a(z)	X
a(z) ≤ \|X\| < 1.0	zSINH(X) is computed using apower series expansion in \|X\| ²
1.0 ≤ \|X\| < b(z)	(zEXP(X) - zEXP(-X))/2
b(z) ≤ \|X\| < c(z)	SIGN(X)*zEXP(\|X\|)/2
c(z) ≤ \|X\|	Overflow occurs

See MTH$HSINH for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$HTANH routine encountered a floating-point reserved operand (a floating-point datum with a sign bit of 1 and a biased exponent of 0) due to incorrect user input. Floating-point reserved operands are reserved for use by VSI.

MTH$_FLOOVEMAT

Floating-point overflow in Math Library: the absolute value of floating-point-input-value is greater than yyy. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

The values of yyy are approximately:

MTH$SINH---88.722
MTH$DSINH---88.722
MTH$GSINH---709.782

MTH$xSQRT

MTH$xSQRT — Square Root. The Square Root routine returns the square root of the input value floating- point-input-value.

Format

MTH$SQRT floating-point-input-value

MTH$DSQRT floating-point-input-value

MTH$GSQRT floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$SQRT_R3

MTH$DSQRT_R5

MTH$GSQRT_R5

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The square root of floating-point-input-value. MTH$SQRT returns an F-floating number. MTH$DSQRT returns a D-floating number. MTH$GSQRT returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

Input value. The floating-point-input-value argument is the address of a floating-point number that contains this input value. For MTH$SQRT, floating-point-input-value specifies an F-floating number. For MTH$DSQRT, floating-point-input-value specifies a D-floating number. For MTH$GSQRT, floating-point-input-value specifies a G-floating number.

Description

The square root of X is computed as follows:

If X < 0 , an error is signaled.

Let X = 2 ^K * F

where:

K is the exponential part of the floating-point data

F is the fractional part of the floating-point data

If K is even:

X = 2 ^(2*P) * F,
zSQRT(X) = 2 ^P * zSQRT(F),
1/2 ≤ F < 1 , where P = K/2

If K is odd:

X = 2 ^(2*P+1) * F = 2 ^(2*P+2) * (F/2),
zSQRT(X) = 2 ^(P+1) * zSQRT(F/2),
1/4 ≤ F/2 < 1/2 , where p = (K-1)/2

Let F' = A*F + B, when K is even:

A = 0.95F6198 (hex)

B = 0.6BA5918 (hex)

Let F' = A* (F/2) + B, when K is odd:

A = 0.D413CCC (hex)

B = 0.4C1E248 (hex)

Let K' = P, when K is even

Let K' = P+1, when K is odd

Let Y[0] = 2^K' * F' be a straight line approximation within the given interval using coefficients A and B which minimize the absolute error at the midpoint and endpoint.

Starting with Y[0], n Newton-Raphson iterations are performed:

Y[n+1] = 1/2 * (Y[n] + X/Y[n])

where n = 2, 3, or 3 for z = F-floating, D-floating, or G-floating, respectively.

See MTH$HSQRT for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xSQRT routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_SQUROONEG	Square root of negative number. Argument floating-point-input-value is less than 0.0. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xTAN

MTH$xTAN — Tangent of Angle Expressed in Radians. The Tangent of Angle Expressed in Radians routine returns the tangent of a given angle (in radians).

Format

MTH$TAN angle-in-radians

MTH$DTAN angle-in-radians

MTH$GTAN angle-in-radians

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$TAN_R4

MTH$DTAN_R7

MTH$GTAN_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The tangent of the angle specified by angle-in-radians. MTH$TAN returns an F-floating number. MTH$DTAN returns a D-floating number. MTH$GTAN returns a G-floating number.

Argument

angle-in-radians

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input angle (in radians). The angle-in-radians argument is the address of a floating-point number that is this angle. For MTH$TAN, angle-in-radians specifies an F-floating number. For MTH$DTAN, angle-in-radians specifies a D-floating number. For MTH$GTAN, angle-in-radians specifies a G-floating number.

Description

When the input argument is expressed in radians, the tangent function is computed as follows:

If |X| < 2^(-f/2) , then zTAN(X) = X (see the section on MTH$zCOSH for the definition of f)
Otherwise, call MTH$zSINCOS to obtain zSIN(X) and zCOS(X); then
1. If zCOS(X) = 0 , signal overflow
2. Otherwise, zTAN(X) = zSIN(X)/zCOS(X)

See MTH$HTAN for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xTAN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library.

MTH$TAND

MTH$TAND — Tangent of Angle Expressed in Degrees. The Tangent of Angle Expressed in Degrees routine returns the tangent of a given angle (in degrees).

Format

MTH$TAND angle-in-degrees

MTH$DTAND angle-in-degrees

MTH$GTAND angle-in-degrees

Each of the above formats accepts one of the floating-point types as input.

Corresponding JSB Entry Points

MTH$TAND_R4

MTH$DTAND_R7

MTH$GTAND_R7

Each of the above JSB entry points accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

Tangent of the angle specified by angle-in-degrees. MTH$TAND returns an F-floating number. MTH$DTAND returns a D-floating number. MTH$GTAND returns a G-floating number.

Argument

angle-in-degrees

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input angle (in degrees). The angle-in-degrees argument is the address of a floating-point number which is this angle. For MTH$TAND, angle-in-degrees specifies an F-floating number. For MTH$DTAND, angle-in-degrees specifies a D-floating number. For MTH$GTAND, angle-in-degrees specifies a G-floating number.

Description

When the input argument is expressed in degrees, the tangent function is computed as follows:

If |X| < (180/π)*2^(-2/(e-1)) and underflow signaling is enabled, underflow is signaled. (See the section on MTH$zCOSH for the definition of e.)
Otherwise, if |X| < (180/π)*2^(-f/2), then zTAND(X) = (π/180)*X. (See the description of MTH$zCOSH for the definition of f.)
Otherwise, call MTH$zSINCOSD to obtain zSIND(X) and zCOSD(X).
1. Then, if zCOSD(X) = 0 , signal overflow
2. Else, zTAND(X) = zSIND(X)/zCOSD(X)

See MTH$HTAND for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND	Reserved operand. The MTH$xTAND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.
MTH$_FLOOVEMAT	Floating-point overflow in Math Library.
MTH$_FLOUNDMAT	Floating-point underflow in Math Library.

MTH$xTANH

MTH$xTANH — Compute the Hyperbolic Tangent. The Compute the Hyperbolic Tangent routine returns the hyperbolic tangent of the input value.

Format

MTH$TANH floating-point-input-value

MTH$DTANH floating-point-input-value

MTH$GTANH floating-point-input-value

Each of the above formats accepts one of the floating-point types as input.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	write only
mechanism:	by value

The hyperbolic tangent of floating-point-input-value. MTH$TANH returns an F-floating number. MTH$DTANH returns a D-floating number. MTH$GTANH returns a G-floating number.

Argument

floating-point-input-value

OpenVMS usage:	floating_point
type:	F_floating, D_floating, G_floating
access:	read only
mechanism:	by reference

The input value. The floating-point-input-value argument is the address of a floating-point number that contains this input value. For MTH$TANH, floating-point-input-value specifies an F-floating number. For MTH$DTANH, floating-point-input-value specifies a D-floating number. For MTH$GTANH, floating-point-input-value specifies a G-floating number.

Description

In calculating the hyperbolic tangent of x, the values of g and h are:

z	g	h
F	12	10
D	28	21
G	26	20

For MTH$TANH, MTH$DTANH, and MTH$GTANH the hyperbolic tangent of x is then computed as follows:

Value of x	Hyperbolic Tangent Returned
\|x\| ≤ 2 ^-g	X
2 ^-g < \|X\| < 0.5	xTANH(X) = X + X ³ * R(X ²), where R(X ²) is a rational function of X ².
0.5 ≤ \|X\| < 1.0	xTANH(X) = xTANH(xHI) + xTANH(xLO)*C/B
	where C = 1 - xTANH(xHI)*xTANH(xHI),
	B = 1 + xTANH(xHI)*xTANH(xLO),
	xHI = 1/2 + N/16 + 1/32 for N=0,1,...,7,
	and xLO = X - xHI.
1.0 < \|X\| < h	xTANH(X) = (xEXP(2X) - 1)/(xEXP(2X) + 1)
h ≤ \|X\|	xTANH(X) = sign(X) *1

See MTH$HTANH for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND

Reserved operand. The MTH$xTANH routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by VSI.

MTH$UMAX

MTH$UMAX — Compute Unsigned Maximum. The Compute Unsigned Maximum routine computes the unsigned longword maximum of n unsigned longword arguments, where n is greater than or equal to 1.

Format

MTH$UMAX argument [argument,...]

Returns

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	write only
mechanism:	by value

Maximum value returned by MTH$UMAX.

Argument

argument

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	read only
mechanism:	by reference

Argument whose maximum MTH$UMAX computes. Each argument argument is an unsigned longword that contains one of these values.

argument

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	read only
mechanism:	by reference

Additional arguments whose maximum MTH$UMAX computes. Each argument argument is an unsigned longword that contains one of these values.

Description

MTH$UMAX is the unsigned version of MTH$JMAX0, and computes the unsigned longword maximum of n unsigned longword arguments, where n is greater than or equal to 1.

Condition Values Signaled

None.

MTH$UMIN

MTH$UMIN — Compute Unsigned Minimum. The Compute Unsigned Minimum routine computes the unsigned longword minimum of n unsigned longword arguments, where n is greater than or equal to 1.

Format

MTH$UMIN argument [argument,...]

Returns

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	write only
mechanism:	by value

Minimum value returned by MTH$UMIN.

Argument

argument

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	read only
mechanism:	by reference

Argument whose minimum MTH$UMIN computes. Each argument argument is an unsigned longword that contains one of these values.

argument

OpenVMS usage:	longword_unsigned
type:	longword (unsigned)
access:	read only
mechanism:	by reference

Additional arguments whose minimum MTH$UMIN computes. Each argument argument is an unsigned longword that contains one of these values.

Description

MTH$UMIN is the unsigned version of MTH$JMIN0, and computes the unsigned longword minimum of n unsigned longword arguments, where n is greater than or equal to 1.

Condition Values Signaled

None.

Chapter 4. Vector MTH$ Reference Section

The Vector MTH$ Reference Section provides detailed descriptions of two sets of vector routines provided by the OpenVMS RTL Mathematics (MTH$) Facility, BLAS Level 1 and FOLR. The BLAS Level 1 are the Basic Linear Algebraic Subroutines designed by Lawson, Hanson, Kincaid, and Krogh (1978). The FOLR (First Order Linear Recurrence) routines provide a vectorized algorithm for the linear recurrence relation.

BLAS1$VIxAMAX

BLAS1$VIxAMAX — Obtain the Index of the First Element of a Vector Having the Largest Absolute Value. The Obtain the Index of the First Element of a Vector Having the Largest Absolute Value routine finds the index of the first occurrence of a vector element having the maximum absolute value.

Format

BLAS1$VISAMAX n ,x ,incx

BLAS1$VIDAMAX n ,x ,incx

BLAS1$VIGAMAX n ,x ,incx

BLAS1$VICAMAX n ,x ,incx

BLAS1$VIZAMAX n ,x ,incx

BLAS1$VIWAMAX n ,x ,incx

Use BLAS1$VISAMAX for single-precision real operations.

Use BLAS1$VIDAMAX for double-precision real (D-floating) operations.

Use BLAS1$VIGAMAX for double-precision real (G-floating) operations.

Use BLAS1$VICAMAX for single-precision complex operations.

Use BLAS1$VIZAMAX for double-precision complex (D-floating) operations.

Use BLAS1$VIWAMAX for double-precision complex (G-floating) operations.

Returns

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	write only
mechanism:	by value

For the real versions of this routine, the function value is the index of the first occurrence of a vector element having the maximum absolute value, as follows:

|x[i]| = max {|x[j]| for j=1,2,...,n}

For the complex versions of this routine, the function value is the index of the first occurrence of a vector element having the largest sum of the absolute values of the real and imaginary parts of the vector elements, as follows:

|Re(x[i])| + |Im(x[i])|= max {|Re(x[j])| + |Im(x[j])| for j=1,2,...,n}

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x. The n argument is the address of a signed longword integer containing the number of elements. If you specify a negative value or 0 for n, 0 is returned.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. This argument is an array of length at least:

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VISAMAX	F-floating real
BLAS1$VIDAMAX	D-floating real
BLAS1$VIGAMAX	G-floating real
BLAS1$VICAMAX	F-floating complex
BLAS1$VIZAMAX	D-floating complex
BLAS1$VIWAMAX	G-floating complex

If n is less than or equal to 0, then imax is 0.

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x_i is referenced as:

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

Description

BLAS1$VISAMAX, BLAS1$VIDAMAX, and BLAS1$VIGAMAX find the index, i , of the first occurrence of a vector element having the maximum absolute value. BLAS1$VICAMAX, BLAS1$VIZAMAX, and BLAS1$VIWAMAX find the index, i , of the first occurrence of a vector element having the largest sum of the absolute values of the real and imaginary parts of the vector elements.

Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x is a real or complex single-precision or double- precision (D and G) n -element vector. The vector can be a row or a column of a matrix. Both forward and backward indexing are permitted.

BLAS1$VISAMAX, BLAS1$VIDAMAX, and BLAS1$VIGAMAX determine the smallest integer i of the n -element vector x such that:

|x[i]| = max {|x[j]| for j=1,2,...,n}

BLAS1$VICAMAX, BLAS1$VIZAMAX, and BLAS1$VIWAMAX determine the smallest integer i of the n-element vector x such that:

|Re(x[i])| + |Im(x[i])|= max {|Re(x[j])| + |Im(x[j])| for j=1,2,...,n}

You can use the BLAS1$VIxAMAX routines to obtain the pivots in Gaussian elimination.

The public-domain BLAS Level 1 IxAMAX routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of setting imax equal to 1 using vector operations.

Example

C 
C To obtain the index of the element with the maximum 
C absolute value. 
C 
        INTEGER IMAX,N,INCX 
        REAL X(40) 
        INCX = 2 
        N = 20 
        IMAX = BLAS1$VISAMAX(N,X,INCX)

BLAS1$VxASUM

BLAS1$VxASUM — Obtain the Sum of the Absolute Values of the Elements of a Vector. The Obtain the Sum of the Absolute Values of the Elements of a Vector routine determines the sum of the absolute values of the elements of the n -element vector x.

Format

BLAS1$VSASUM n ,x ,incx

BLAS1$VDASUM n ,x ,incx

BLAS1$VGASUM n ,x ,incx

BLAS1$VSCASUM n ,x ,incx

BLAS1$VDZASUM n ,x ,incx

BLAS1$VGWASUM n ,x ,incx

Use BLAS1$VSASUM for single-precision real operations.

Use BLAS1$VDASUM for double-precision real (D-floating) operations.

Use BLAS1$VGASUM for double-precision real (G-floating) operations.

Use BLAS1$VSCASUM for single-precision complex operations.

Use BLAS1$VDZASUM for double-precision complex (D-floating) operations.

Use BLAS1$VGWASUM for double-precision complex (G-floating) operations.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, or G_floating real
access:	write only
mechanism:	by value

The function value, called sum, is the sum of the absolute values of the elements of the vector x. The data type of the function value is a real number; for the BLAS1$VSCASUM, BLAS1$VDZASUM, and BLAS1$VGWASUM routines, the data type of the function value is the real data type corresponding to the complex argument data type.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x to be added. The n argument is the address of a signed longword integer containing the number of elements.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSASUM	F-floating real
BLAS1$VDASUM	D-floating real
BLAS1$VGASUM	G-floating real
BLAS1$VSCASUM	F-floating complex
BLAS1$VDZASUM	D-floating complex
BLAS1$VGWASUM	G-floating complex

If n is less than or equal to 0, then sum is 0.0.

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If you specify a negative value for incx , it is interpreted as the absolute value of incx.

Description

BLAS1$VSASUM, BLAS1$VDASUM, and BLAS1$VGASUM obtain the sum of the absolute values of the elements of the n -element vector x. BLAS1$VSCASUM, BLAS1$VDZASUM, and BLAS1$VGWASUM obtain the sum of the absolute values of the real and imaginary parts of the elements of the n -element vector x.

BLAS1$VSASUM, BLAS1$VDASUM, and BLAS1$VGASUM compute the sum of the absolute values of the elements of x, which is expressed as follows:

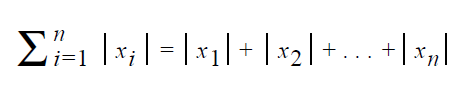
BLAS1$VSCASUM, BLAS1$VDZASUM, and BLAS1$VGWASUM compute the sum of the absolute values of the real and imaginary parts of the elements of x , which is expressed as follows:

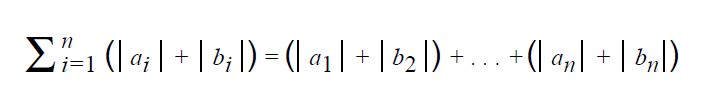
where | x_i | = (a_i, b_i)

and | a_i | + | b_i | = | real | + | imaginary |

The public-domain BLAS Level 1 xASUM routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of computing n*|x₁| using vector operations.

Rounding in the summation occurs in a different order than in a sequential evaluation of the sum, so the final result may differ from the result of a sequential evaluation.

Example

C 
C To obtain the sum of the absolute values of the 
C elements of vector x: 
C 
        INTEGER N,INCX 
        REAL X(20),SUM 
        INCX = 1 
        N = 20 
        SUM = BLAS1$VSASUM(N,X,INCX)

BLAS1$VxAXPY

BLAS1$VxAXPY — Multiply a Vector by a Scalar and Add a Vector. The Multiply a Vector by a Scalar and Add a Vector routine computes ax + y, where a is a scalar number and x and y are n -element vectors.

Format

BLAS1$VSAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VDAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VGAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VCAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VZAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VWAXPY n ,a ,x ,incx ,y ,incy

Use BLAS1$VSAXPY for single-precision real operations.

Use BLAS1$VDAXPY for double-precision real (D-floating) operations.

Use BLAS1$VGAXPY for double-precision real (G-floating) operations.

Use BLAS1$VCAXPY for single-precision complex operations.

Use BLAS1$VZAXPY for double-precision complex (D-floating) operations.

Use BLAS1$VWAXPY for double-precision complex (G-floating) operations.

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vectors x and y. The n argument is the address of a signed longword integer containing the number of elements. If n is less than or equal to 0, then y is unchanged.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

Scalar multiplier for the array x. The a argument is the address of a floating-point or floating-point complex number that is this multiplier. If a equals 0, then y is unchanged. If a shares a memory location with any element of the vector y , results are unpredictable. Specify the same data type for arguments a, x, and y.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSAXPY	F-floating real
BLAS1$VDAXPY	D-floating real
BLAS1$VGAXPY	G-floating real
BLAS1$VCAXPY	F-floating complex
BLAS1$VZAXPY	D-floating complex
BLAS1$VWAXPY	G-floating complex

If any element of x shares a memory location with an element of y, the results are unpredictable.

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; ) that is, x_i is referenced in:

x(1+(n-i)*|incx|)

where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

On entry, array containing the elements to be accessed. All elements of array y are accessed only if the increment argument of y, called incy, is 1. The y argument is the address of a floating-point or floating-point complex number that is this array. The length of this array is at least:

1+(n-1)*|incy|

where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

Specify the data type as follows:

Routine	Data Type for y
BLAS1$VSAXPY	F-floating real
BLAS1$VDAXPY	D-floating real
BLAS1$VGAXPY	G-floating real
BLAS1$VCAXPY	F-floating complex
BLAS1$VZAXPY	D-floating complex
BLAS1$VWAXPY	G-floating complex

If n is less than or equal to 0, then y is unchanged. If any element of x shares a memory location with an element of y, the results are unpredictable.

On exit, y contains an array of length at least:

1+(n-1)*|incy|

where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

After the call to BLAS1$VxAXPY, ui is set equal to:

y_i+a*x_i

where:

y = the vector y

i = element of the vector x or y

a = scalar multiplier for the vector x specified in a

x = the vector x

incy

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array y. The incy argument is the address of a signed longword integer containing the increment argument. If incy is greater than or equal to 0, then y is referenced forward in array y; that is, y_i is referenced in:

y(1+(i-1)*incy)

where:

y = array specified in y

i = element of the vector y

incy = increment argument for the array y specified in incy

If incy is less than 0, then y is referenced backward in array y ; that is, y_i is is referenced in:

y(1+(n-i)*|incy|)

where:

y = array specified in y

n = number of vector elements specified in n

i = element of the vector y

incy = increment argument for the array y specified in incy

Description

BLAS1$VxAXPY multiplies a vector x by a scalar, adds to a vector y, and stores the result in the vector y. This is expressed as follows:

y ← ax + y

where a is a scalar number and x and y are real or complex single-precision or double-precision (D and G) n -element vectors. The vectors can be rows or columns of a matrix. Both forward and backward indexing are permitted. Vectors x and y contain n elements that are accessed from arrays x and y by stepping incx and incy elements at a time.

The routine name determines the data type you should specify for arguments a , x , and y. Specify the same data type for each of these arguments.

The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of adding the constant a * x₁ to all elements of the vector y using vector operations.

Example

C 
C To compute y=y+2.0*x using SAXPY: 
C 
        INTEGER N,INCX,INCY 
        REAL X(20), Y(20),A 
        INCX = 1 
        INCY = 1 
        A = 2.0 
        N = 20 
        CALL BLAS1$VSAXPY(N,A,X,INCX,Y,INCY)

BLAS1$VxCOPY

BLAS1$VxCOPY — Copy a Vector. The Copy a Vector routine copies n elements of the vector x to the vector y.

Format

BLAS1$VSCOPY n ,x ,incx ,y ,incy

BLAS1$VDCOPY n ,x ,incx ,y ,incy

BLAS1$VCCOPY n ,x ,incx ,y ,incy

BLAS1$VZCOPY n ,x ,incx ,y ,incy

Use BLAS1$VSCOPY for single-precision real operations.

Use BLAS1$VDCOPY for double-precision real (D or G) operations.

Use BLAS1$VCCOPY for single-precision complex operations.

Use BLAS1$VZCOPY for double-precision complex (D or G) operations.

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x to be copied. The n argument is the address of a signed longword integer containing the number of elements in vector x. If n is less than or equal to 0, then y is unchanged.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSCOPY	F-floating real
BLAS1$VDCOPY	D-floating or G-floating real
BLAS1$VCCOPY	F-floating complex
BLAS1$VZCOPY	D-floating or G-floating complex

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; that is, x_i is referenced in:

x(1+(n-i)*|incx|)

where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

Array that receives the copied elements. All elements of array y receive the copied elements only if the increment argument of y, called incy, is 1. The y argument is the address of a floating-point or floating-point complex number that is this array. This argument is an array of length at least:

1+(n-1)*|incy|

where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

Specify the data type as follows:

Routine	Data Type for y
BLAS1$VSCOPY	F-floating real
BLAS1$VDCOPY	D-floating or G-floating real
BLAS1$VCCOPY	F-floating complex
BLAS1$VZCOPY	D-floating or G-floating complex

If n is less than or equal to 0, then y is unchanged. If incx is equal to 0, then each y_i is set to x₁. If incy is equal to 0, then y_i is set to the last referenced element of x. If any element of x shares a memory location with an element of y, the results are unpredictable. (See the Description section for a special case that does not cause unpredictable results when the same memory location is shared by input and output.)

incy

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array y. The incy argument is the address of a signed longword integer containing the increment argument. If incy is greater than or equal to 0, then _y is referenced forward in array y; that is, y_i is referenced in:

y(1+(i-1)*incy)

where:

y = array specified in y

i = element of the vector y

If incy is less than 0, then y is referenced backward in array y; that is, y_i is referenced in:

y(1+(n-i)*|incy|)

where:

y = array specified in y

n = number of vector elements specified in n

i = element of the vector y

incy = increment argument for the array y specified in incy

Description

BLAS1$VSCOPY, BLAS1$VDCOPY, BLAS1$VCCOPY, and BLAS1$VZCOPY copy n elements of the vector x to the vector y. Vector x contains n elements that are accessed from array x by stepping incx elements at a time. Both x and y are real or complex single-precision or double-precision (D and G) n-element vectors. The vectors can be rows or columns of a matrix. Both forward and backward indexing are permitted.

If you specify 0 for incx , BLAS1$VxCOPY initializes all elements of y to a constant.

If you specify –incx for incy, the vector x is stored in reverse order in y. In this case, the call format is as follows:

CALL BLAS1$VxCOPY (N,X,INCX,Y,-INCX)

It is possible to move the contents of a vector up or down within itself and not cause unpredictable results even though the same memory location is shared between input and output. To do this when i is greater than j , call the routine BLAS1$VxCOPY with incx = incy > 0 as follows:

CALL BLAS1$VxCOPY (N,X(I),INCX,X(J),INCX)

The preceding call to BLAS1$VxCOPY moves:

x(i),x(i+1*incx),...x(i+(n-1)*incx)

x(j),x(j+1*incx),...x(j+(n-1)*incx)

If i is less than j , specify a negative value for incx and incy in the call to BLAS1$VxCOPY, as follows. The parts that do not overlap are unchanged.

CALL BLAS1$VxCOPY (N,X(I),-INCX,X(J),-INCX)

Note

BLAS1$VxCOPY does not perform floating operations on the input data. Therefore, floating reserved operands are not detected by BLAS1$VxCOPY.

Example

C 
C To copy a vector x to a vector y using BLAS1$VSCOPY: 
C 
        INTEGER N,INCX,INCY 
        REAL X(20),Y(20) 
        INCX = 1 
        INCY = 1 
        N = 20 
        CALL BLAS1$VSCOPY(N,X,INCX,Y,INCY) 
C 
C To move the contents of X(1),X(3),X(5),...,X(2N-1) 
C to X(3),X(5),...,X(2N+1) and leave x unchanged: 
C 
        CALL BLAS1$VSCOPY(N,X,-2,X(3),-2)) 
C 
C To move the contents of X(2),X(3),...,X(100) to 
C X(1),X(2),...,X(99)and leave x(100) unchanged: 
C 
        CALL BLAS1$VSCOPY(99,X(2),1,X,1)) 
C 
C To move the contents of X(1),X(2),X(3),...,X(N) to 
C Y(N),Y(N-1),...,Y 
C 
        CALL BLAS1$VSCOPY(N,X,1,Y,-1))

BLAS1$VxDOTx

BLAS1$VxDOTx — Obtain the Inner Product of Two Vectors. The Obtain the Inner Product of Two Vectors routine returns the dot product of two n -element vectors, x and y.

Format

BLAS1$VSDOT n ,x ,incx ,y ,incy

BLAS1$VDDOT n ,x ,incx ,y ,incy

BLAS1$VGDOT n ,x ,incx ,y ,incy

BLAS1$VCDOTU n ,x ,incx ,y ,incy

BLAS1$VCDOTC n ,x ,incx ,y ,incy

BLAS1$VZDOTU n ,x ,incx ,y ,incy

BLAS1$VWDOTU n ,x ,incx ,y ,incy

BLAS1$VZDOTC n ,x ,incx ,y ,incy

BLAS1$VWDOTC n ,x ,incx ,y ,incy

Use BLAS1$VSDOT to obtain the inner product of two single-precision real vectors.

Use BLAS1$VDDOT to obtain the inner product of two double-precision (D- floating) real vectors.

Use BLAS1$VGDOT to obtain the inner product of two double-precision (G-floating) real vectors.

Use BLAS1$VCDOTU to obtain the inner product of two single-precision complex vectors (unconjugated).

Use BLAS1$VCDOTC to obtain the inner product of two single-precision complex vectors (conjugated).

Use BLAS1$VZDOTU to obtain the inner product of two double-precision (D- floating) complex vectors (unconjugated).

Use BLAS1$VWDOTU to obtain the inner product of two double-precision (G-floating) complex vectors (unconjugated).

Use BLAS1$VZDOTC to obtain the inner product of two double-precision (D- floating) complex vectors (conjugated).

Use BLAS1$VWDOTC to obtain the inner product of two double-precision (G-floating) complex vectors (conjugated).

Returns

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	write only
mechanism:	by value

The function value, called dotpr, is the dot product of two n-element vectors, x and y. Specify the same data type for dotpr and the argument x.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x to be copied. The n argument is the address of a signed longword integer containing the number of elements. If you specify a value for n that is less than or equal to 0, then the value for dotpr is 0.0.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSDOT	F-floating real
BLAS1$VDDOT	D-floating real
BLAS1$VGDOT	G-floating real
BLAS1$VCDOTU and BLAS1$VCDOTC	F-floating complex
BLAS1$VZDOTU and BLAS1$VZDOTC	D-floating complex
BLAS1$VWDOTU and BLAS1$VWDOTC	G-floating complex

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; that is, x_i is referenced in:

x(1+(n-i)*|incx|)

where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

Array containing the elements to be accessed. All elements of array y are accessed only if the increment argument of y, called incy, is 1. The y argument is the address of a floating-point or floating-point complex number that is this array. This argument is an array of length at least:

1+(n-1)*|incy|

where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

Specify the data type as follows:

Routine	Data Type for y
BLAS1$VSDOT	F-floating real
BLAS1$VDDOT	D-floating real
BLAS1$VGDOT	G-floating real
BLAS1$VCDOTU and BLAS1$VCDOTC	F-floating complex
BLAS1$VZDOTU and BLAS1$VZDOTC	D-floating complex
BLAS1$VWDOTU and BLAS1$VWDOTC	G-floating complex

incy

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array y. The incy argument is the address of a signed longword integer containing the increment argument. If incy is greater than or equal to 0, then _y is referenced forward in array y; that is, y_i is referenced in:

y(1+(i-1)*incy)

where:

y = array specified in y

i = element of the vector y

incy = increment argument for the array y specified in incy

If incy is less than 0, then y is referenced backward in array y; that is, y_i is referenced in:

y(1+(n-i)*|incy|)

where:

y = array specified in y

n = number of vector elements specified in n

i = element of the vector y

incy = increment argument for the array y specified in incy

Description

The unconjugated versions of this routine, BLAS1$VSDOT, BLAS1$VDDOT, BLAS1$VGDOT, BLAS1$VCDOTU, BLAS1$VZDOTU, and BLAS1$VWDOTU return the dot product of two n -element vectors, x and y, expressed as follows:

x· y = x₁y₁ + x₂y₂ + ... + x_ny_n

The conjugated versions of this routine, BLAS1$VCDOTC, BLAS1$VZDOTC, and BLAS1$VWDOTC return the dot product of the conjugate of the first n -element vector with a second n -element vector, as follows:

x̄· y = x̄₁y₁ + x̄₂y₂ + ... + x̄_ny_n

Vectors x and y contain n elements that are accessed from arrays x and y by stepping incx and incy elements at a time. The vectors x and y can be rows or columns of a matrix. Both forward and backward indexing are permitted.

The routine name determines the data type you should specify for arguments x and y. Specify the same data type for these arguments.

Rounding in BLAS1$VxDOTx occurs in a different order than in a sequential evaluation of the dot product. The final result may differ from the result of a sequential evaluation.

Example

C 
C To compute the dot product of two vectors, x and y, 
C and return the result in DOTPR: 
C 
        INTEGER INCX,INCY 
        REAL X(20),Y(20),DOTPR 
        INCX = 1 
        INCY = 1 
        N = 20 
        DOTPR = BLAS1$VSDOT(N,X,INCX,Y,INCY)

BLAS1$VxNRM2

BLAS1$VxNRM2 — Obtain the Euclidean Norm of a Vector. The Obtain the Euclidean Norm of a Vector routine obtains the Euclidean norm of an n -element vector x, expressed in the following figure.

Figure

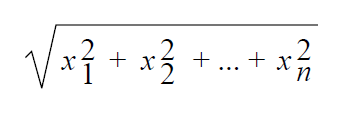
Format

BLAS1$VSNRM2 n ,x ,incx

BLAS1$VDNRM2 n ,x ,incx

BLAS1$VGNRM2 n ,x ,incx

BLAS1$VSCNRM2 n ,x ,incx

BLAS1$VDZNRM2 n ,x ,incx

BLAS1$VGWNRM2 n ,x ,incx

Use BLAS1$VSNRM2 for single-precision real operations.

Use BLAS1$VDNRM2 for double-precision real (D-floating) operations.

Use BLAS1$VGNRM2 for double-precision real (G-floating) operations.

Use BLAS1$VSCNRM2 for single-precision complex operations.

Use BLAS1$VDZNRM2 for double-precision complex (D-floating) operations.

Use BLAS1$VGWNRM2 for double-precision complex (G-floating) operations.

Returns

OpenVMS usage:	floating_point
type:	F_floating, D_floating, or G_floating real
access:	write only
mechanism:	by value

The function value, called e_norm, is the Euclidean norm of the vector x. The data type of the function value is a real number; for the BLAS1$VSCNRM2, BLAS1$VDZNRM2, and BLAS1$VGWNRM2 routines, the data type of the function value is the real data type corresponding to the complex argument data type.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x to be processed. The n argument is the address of a signed longword integer containing the number of elements.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSNRM2	F-floating real
BLAS1$VDNRM2	D-floating real
BLAS1$VGNRM2	G-floating real
BLAS1$VSCNRM2	F-floating complex
BLAS1$VDZNRM2	D-floating complex
BLAS1$VGWNRM2	G-floating complex

If n is less than or equal to 0, then e_norm is 0.0.

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If you specify a negative value for incx, it is interpreted as the absolute value of incx.

Description

BLAS1$VxNRM2 obtains the Euclidean norm of an n-element vector x, expressed as follows:

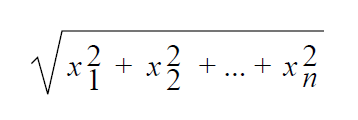
Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x is a real or complex single-precision or double-precision (D and G) n-element vector. The vector can be a row or a column of a matrix. Both forward and backward indexing are permitted.

The public-domain BLAS Level 1 xNRM2 routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of using vector operations to set e_norm as follows:

e_norm = n^0.5 * |x₁|

For BLAS1$VDNRM2, BLAS1$VGNRM2, BLAS1$VDZNRM2, and BLAS1$VGWNRM2 (the double-precision routines), the elements of the vector x are scaled to avoid intermediate overflow or underflow. BLAS1$VSNRM2 and BLAS1$VSCNRM2 (the single-precision routines) use a backup data type to avoid intermediate overflow or underflow.

Rounding in BLAS1$VxNRM2 occurs in a different order than in a sequential evaluation of the Euclidean norm. The final result may differ from the result of a sequential evaluation.

Example

C 
C To obtain the Euclidean norm of the vector x: 
C 
        INTEGER INCX,N 
        REAL X(20),E_NORM 
        INCX = 1 
        N = 20 
        E_NORM = BLAS1$VSNRM2(N,X,INCX)

BLAS1$VxROT

BLAS1$VxROT — Apply a Givens Plane Rotation. The Apply a Givens Plane Rotation routine applies a Givens plane rotation to a pair of n -element vectors x and y.

Format

BLAS1$VSROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VDROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VGROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VCSROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VZDROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VWGROT n ,x ,incx ,y ,incy ,c ,s

Use BLAS1$VSROT for single-precision real operations.

Use BLAS1$VDROT for double-precision real (D-floating) operations.

Use BLAS1$VGROT for double-precision real (G-floating) operations.

Use BLAS1$VCSROT for single-precision complex operations.

Use BLAS1$VZDROT for double-precision complex (D-floating) operations.

Use BLAS1$VWGROT for double-precision complex (G-floating) operations.

BLAS1$VCSROT, BLAS1$VZDROT, and BLAS1$VWGROT are real rotations applied to a complex vector.

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vectors x and y to be rotated. The n argument is the address of a signed longword integer containing the number of elements to be rotated. If n is less than or equal to 0, then x and y are unchanged.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSROT	F-floating real
BLAS1$VDROT	D-floating real
BLAS1$VGROT	G-floating real
BLAS1$VCSROT	F-floating complex
BLAS1$VZDROT	D-floating complex
BLAS1$VWGROT	G-floating complex

If n is less than or equal to 0, then x and y are unchanged. If c equals 1.0 and s equals 0, then x and y are unchanged. If any element of x shares a memory location with an element of y, then the results are unpredictable.

On exit, x contains the rotated vector x , as follows:

x_i ← c * x_i + s * y_i

where:

x = array x specified in x

y = array y specified in y

i = i = 1,2,…,n

c = rotation element generated by the BLAS1$VxROTG routines

s = rotation element generated by the BLAS1$VxROTG routines

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; that is, x_i is referenced in:

x(1+(n-i)*|incx|)

where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for y
BLAS1$VSROT	F-floating real
BLAS1$VDROT	D-floating real
BLAS1$VGROT	G-floating real
BLAS1$VCSROT	F-floating complex
BLAS1$VZDROT	D-floating complex
BLAS1$VWGROT	G-floating complex

On exit, y contains the rotated vector y , as follows:

y_i ← - s * x_i + c * y_i

where:

x = array x specified in x

y = array y specified in y

i = i = 1,2,…,n

c = real rotation element (can be generated by the BLAS1$VxROTG routines)

s = complex rotation element (can be generated by the BLAS1$VxROTG routines)

incy

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

y(1+(i-1)*incy)

where:

y = array specified in y

i = element of the vector y

incy = increment argument for the array y specified in incy

If incy is less than 0, then y is referenced backward in array y; that is, y_i is referenced in:

y(1+(n-i)*|incy|)

where:

y = array specified in y

n = number of vector elements specified in n

i = element of the vector y

incy = increment argument for the array y specified in incy

OpenVMS usage:	floating_point
type:	F_floating, D_floating, or G_floating real
access:	read only
mechanism:	by reference

First rotation element, which can be interpreted as the cosine of the angle of rotation. The c argument is the address of a floating-point or floating-point complex number that is this vector element. The c argument is the first rotation element generated by the BLAS1$VxROTG routines.

Specify the data type (which is always real) as follows:

Routine	Data Type for c
BLAS1$VSROT and BLAS1$VCSROT	F-floating real
BLAS1$VDROT and BLAS1$VZDROT	D-floating real
BLAS1$VGROT and BLAS1$VWGROT	G-floating real

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference

Second rotation element, which can be interpreted as the sine of the angle of rotation. The s argument is the address of a floating-point or floating-point complex number that is this vector element. The s argument is the second rotation element generated by the BLAS1$VxROTG routines.

Specify the data type (which can be either real or complex) as follows:

Routine	Data Type for s
BLAS1$VSROT and BLAS1$VCSROT	F-floating real or F-floating complex
BLAS1$VDROT and BLAS1$VZDROT	D-floating real or D-floating complex
BLAS1$VGROT and BLAS1$VWGROT	G-floating real or G-floating complex

Description

BLAS1$VSROT, BLAS1$VDROT, and BLAS1$VGROT apply a real Givens plane rotation to a pair of real vectors. BLAS1$VCSROT, BLAS1$VZDROT, and BLAS1$VWGROT apply a real Givens plane rotation to a pair of complex vectors. The vectors x and y are real or complex single-precision or double-precision (D and G) vectors. The vectors can be rows or columns of a matrix. Both forward and backward indexing are permitted. The routine name determines the data type you should specify for arguments x and y. Specify the same data type for each of these arguments.

The Givens plane rotation is applied to n elements, where the elements to be rotated are contained in vectors x and y (i equals 1,2,...,n). These elements are accessed from arrays x and y by stepping incx and incy elements at a time. The cosine and sine of the angle of rotation are c and s, respectively. The arguments c and s are usually generated by the BLAS Level 1 routine BLAS1$VxROTG, using a=x and b=y:

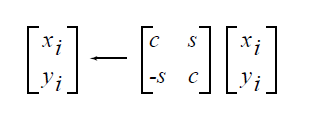
The BLAS1$VxROT routines can be used to introduce zeros selectively into a matrix.

Example

C 
C To rotate the first two rows of a matrix and zero 
C out the element in the first column of the second row: 
C 
        INTEGER INCX,N 
        REAL X(20,20),A,B,C,S 
        INCX = 20 
        N = 20 
        A = X(1,1) 
        B = X(2,1) 
        CALL BLAS1$VSROTG(A,B,C,S) 
        CALL BLAS1$VSROT(N,X,INCX,X(2,1),INCX,C,S)

BLAS1$VxROTG

BLAS1$VxROTG — Generate the Elements for a Givens Plane. The Generate the Elements for a Givens Plane Rotation routine constructs a Givens plane rotation that eliminates the second element of a two-element vector.

Format

BLAS1$VSROTG a ,b ,c ,s

BLAS1$VDROTG a ,b ,c ,s

BLAS1$VGROTG a ,b ,c ,s

BLAS1$VCROTG a ,b ,c ,s

BLAS1$VZROTG a ,b ,c ,s

BLAS1$VWROTG a ,b ,c ,s

Use BLAS1$VSROTG for single-precision real operations.

Use BLAS1$VDROTG for double-precision real (D-floating) operations.

Use BLAS1$VGROTG for double-precision real (G-floating) operations.

Use BLAS1$VCROTG for single-precision complex operations.

Use BLAS1$VZROTG for double-precision complex (D-floating) operations.

Use BLAS1$VWROTG for double-precision complex (G-floating) operations.

Returns

None.

Argument

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference

On entry, first element of the input vector. On exit, rotated element r. The a argument is the address of a floating-point or floating-point complex number that is this vector element.

Specify the data type as follows:

Routine	Data Type for a
BLAS1$VSROTG	F-floating real
BLAS1$VDROTG	D-floating real
BLAS1$VGROTG	G-floating real
BLAS1$VCROTG	F-floating complex
BLAS1$VZROTG	D-floating complex
BLAS1$VWROTG	G-floating complex

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference

On entry, second element of the input vector. On exit from BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG, reconstruction element z. (See the Description section for more information about z.) The b argument is the address of a floating-point or floating-point complex number that is this vector element.

Specify the data type as follows:

Routine	Data Type for b
BLAS1$VSROTG	F-floating real
BLAS1$VDROTG	D-floating real
BLAS1$VGROTG	G-floating real
BLAS1$VCROTG	F-floating complex
BLAS1$VZROTG	D-floating complex
BLAS1$VWROTG	G-floating complex

OpenVMS usage:	floating_point
type:	F_floating, D_floating, or G_floating real
access:	write only
mechanism:	by reference

Specify the data type (which is always real) as follows:

Routine	Data Type for c
BLAS1$VSROTG and BLAS1$VCROTG	F-floating real
BLAS1$VDROTG and BLAS1$VZROTG	D-floating real
BLAS1$VGROTG and BLAS1$VWROTG	G-floating real

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	write only
mechanism:	by reference

Second rotation element, which can be interpreted as the sine of the angle of rotation. The s argument is the address of a floating-point or floating-point complex number that is this vector element.

Specify the data type as follows:

Routine	Data Type for s
BLAS1$VSROTG	F-floating real
BLAS1$VDROTG	D-floating real
BLAS1$VGROTG	G-floating real
BLAS1$VCROTG	F-floating complex
BLAS1$VZROTG	D-floating complex
BLAS1$VWROTG	G-floating complex

Description

BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG construct a real Givens plane rotation. BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG construct a complex Givens plane rotation. The Givens plane rotation eliminates the second element of a two-element vector. The elements of the vector are real or complex single-precision or double-precision (D and G) numbers. The routine name determines the data type you should specify for arguments a, b, and s. Specify the same data type for each of these arguments.

BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG can use the reconstruction element z to store the rotation elements for future use. There is no counterpart to the term z for BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG.

The BLAS1$VxROTG routines can be used to introduce zeros selectively into a matrix.

For BLAS1$VDROTG, BLAS1$VGROTG, BLAS1$VZROTG, and BLAS1$VWROTG (the double-precision routines), the elements of the vector are scaled to avoid intermediate overflow or underflow. BLAS1$VSROTG and BLAS1$VCROTG (the single-precision routines) use a backup data type to avoid intermediate underflow or overflow, which may cause the final result to differ from the original Fortran routine.

BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG --- Real Givens Plane Rotation

Given the elements a and b of an input vector, BLAS1$VSROTG, and BLAS1$VDROTG, BLAS1$VGROTG calculate the elements c and s of an orthogonal matrix such that:

A real Givens plane rotation is constructed for values a and b by computing values for r, c, s, and z, as follows:

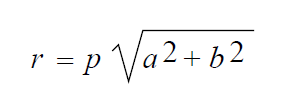
where:
p =SIGN(a) if |a| > |b|
p =SIGN(b) if |a|≤|b|
c = a/r if r ≠ 0
c = 1 if r = 0
s = b/r if r ≠ 0
s = 0 if r = 0
z = s if |a| > |b|
z = 1/c if |a|≤|b| and c ≠ 0 and r ≠ 0
z = 1 if |a|≤|b| and c = 0 and r ≠ 0
z = 0 if r = 0

BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG can use the reconstruction element z to store the rotation elements for future use. The quantities c and s are reconstructed from z as follows:

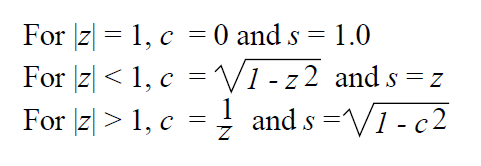
The arguments c and s can be passed to the BLAS1$VxROT routines.

BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG --- Complex Givens Plane Rotation

Given the elements a and b of an input vector, BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG calculate the elements c and s of an orthogonal matrix such that:

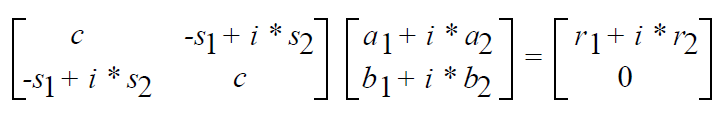
There are no BLAS Level 1 routines with which you can use complex c and s arguments.

Example

C 
C To generate the rotation elements for a vector of 
C elements a and b: 
C 
        REAL A,B,C,S 
        CALL SROTG(A,B,C,S)

BLAS1$VxSCAL

BLAS1$VxSCAL — Scale the Elements of a Vector. The Scale the Elements of a Vector routine computes a * x where a is a scalar number and x is an n -element vector.

Format

BLAS1$VSSCAL n ,a ,x ,incx

BLAS1$VDSCAL n ,a ,x ,incx

BLAS1$VGSCAL n ,a ,x ,incx

BLAS1$VCSCAL n ,a ,x ,incx

BLAS1$VCSSCAL n ,a ,x ,incx

BLAS1$VZSCAL n ,a ,x ,incx

BLAS1$VWSCAL n ,a ,x ,incx

BLAS1$VZDSCAL n ,a ,x ,incx

BLAS1$VWGSCAL n ,a ,x ,incx

Use BLAS1$VSSCAL to scale a real single-precision vector by a real single- precision scalar.

Use BLAS1$VDSCAL to scale a real double-precision (D-floating) vector by a real double-precision (D-floating) scalar.

Use BLAS1$VGSCAL to scale a real double-precision (G-floating) vector by a real double-precision (G-floating) scalar.

Use BLAS1$VCSCAL to scale a complex single-precision vector by a complex single-precision scalar.

Use BLAS1$VCSSCAL to scale a complex single-precision vector by a real single- precision scalar.

Use BLAS1$VZSCAL to scale a complex double-precision (D-floating) vector by a complex double-precision (D-floating) scalar.

Use BLAS1$VWSCAL to scale a complex double-precision (G-floating) vector by a complex double-precision (G-floating) scalar.

Use BLAS1$VZDSCAL to scale a complex double-precision (D-floating) vector by a real double-precision (D-floating) scalar.

Use BLAS1$VWGSCAL to scale a complex double-precision (G-floating) vector by a real double-precision (G-floating) scalar.

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x to be scaled. The n argument is the address of a signed longword integer containing the number of elements to be scaled. If you specify a value for n that is less than or equal to 0, then x is unchanged.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference

Scalar multiplier for the elements of vector x. The a argument is the address of a floating-point or floating-point complex number that is this multiplier.

Specify the data type as follows:

Routine	Data Type for a
BLAS1$VSSCAL and BLAS1$VCSSCAL	F-floating real
BLAS1$VDSCAL and BLAS1$VZDSCAL	D-floating real
BLAS1$VGSCAL and BLAS1$VWGSCAL	G-floating real
BLAS1$VCSCAL	F-floating complex
BLAS1$VZSCAL	D-floating complex
BLAS1$VWSCAL	G-floating complex

If you specify 1.0 for a, then x is unchanged.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSSCAL	F-floating real
BLAS1$VDSCAL	D-floating real
BLAS1$VGSCAL	G-floating real
BLAS1$VCSCAL and BLAS1$VCSSCAL	F-floating complex
BLAS1$VZSCAL and BLAS1$VZDSCAL	D-floating complex
BLAS1$VWSCAL and BLAS1$VWGSCAL	G-floating complex

On exit, x is an array of length at least:

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

y = increment argument for the array x specified in incx

After the call to BLAS1$VxSCAL, x_i is replaced by a * x_i If a shares a memory location with any element of the vector x, results are unpredictable.

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If you specify a negative value for incx, it is interpreted as the absolute value of incx. If incx equals 0, the results are unpredictable.

Description

BLAS1$VxSCAL computes a * x where a is a scalar number and x is an n-element vector. The computation is expressed as follows:

Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x can be a row or a column of a matrix. Both forward and backward indexing are permitted.

The public-domain BLAS Level 1 xSCAL routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for a = 0. Therefore, specifying 0 for a has the effect of setting to zero all elements of the vector x using vector operations.

Example

C 
C To scale a vector x by 2.0 using SSCAL: 
C 
        INTEGER INCX,N 
        REAL X(20),A 
        INCX = 1 
        A = 2 
        N = 20 
        CALL BLAS1$VSSCAL(N,A,X,INCX)

BLAS1$VxSWAP

BLAS1$VxSWAP — Swap the Elements of Two Vectors. The Swap the Elements of Two Vectors routine swaps n elements of the vector x with the vector y.

Format

BLAS1$VSSWAP n ,x ,incx ,y ,incy

BLAS1$VDSWAP n ,x ,incx ,y ,incy

BLAS1$VCSWAP n ,x ,incx ,y ,incy

BLAS1$VZSWAP n ,x ,incx ,y ,incy

Use BLAS1$VSSWAP for single-precision real operations.

Use BLAS1$VDSWAP for double-precision real (D or G) operations.

Use BLAS1$VCSWAP for single-precision complex operations.

Use BLAS1$VZSWAP for double-precision complex (D or G) operations.

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Number of elements in vector x to be swapped. The n argument is the address of a signed longword integer containing the number of elements to be swapped.

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine	Data Type for x
BLAS1$VSSWAP	F-floating real
BLAS1$VDSWAP	D-floating or G-floating real
BLAS1$VCSWAP	F-floating complex
BLAS1$VZSWAP	D-floating or G-floating complex

If n is less than or equal to 0, then x and y are unchanged. If any element of x shares a memory location with an element of y, the results are unpredictable.

On exit, x is an array of length at least:

1+(n-1)*|incx|

where:

n = number of vector elements specified in n

y = increment argument for the array x specified in incx

After the call to BLAS1$VxSWAP, n elements of the array specified by x are interchanged with n elements of the array specified by y.

incx

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

x(1+(i-1)*incx)

where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; that is, x_i is referenced in:

x(1+(n-i)*|incx|)

where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference, array reference

1+(n-1)*|incy|

where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

Specify the data type as follows:

Routine	Data Type for y
BLAS1$VSSWAP	F-floating real
BLAS1$VDSWAP	D-floating or G-floating real
BLAS1$VCSWAP	F-floating complex
BLAS1$VZSWAP	D-floating or G-floating complex

If n is less than or equal to 0, then x and y are unchanged. If any element of x shares a memory location with an element of y, the results are unpredictable.

On exit, y is an array of length at least:

1+(n-1)*|incy|

where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

After the call to BLAS1$VxSWAP, n elements of the array specified by x are interchanged with n elements of the array specified by y.

incy

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

y(1+(i-1)*incy)

where:

y = array specified in y

i = element of the vector y

incy = increment argument for the array y specified in incy

If incy is less than 0, then y is referenced backward in array y; that is, y_i is referenced in:

y(1+(n-i)*|incy|)

where:

y = array specified in y

n = number of vector elements specified in n

i = element of the vector y

incy = increment argument for the array y specified in incy

Description

BLAS1$VSSWAP, BLAS1$VDSWAP, BLAS1$VCSWAP, and BLAS1$VZSWAP swap n elements of the vector x with the vector y. Vectors x and y contain n elements that are accessed from arrays x and y by stepping incx and incy elements at a time. Both x and y are real or complex single-precision or double-precision (D and G) n-element vectors. The vectors can be rows or columns of a matrix. Both forward and backward indexing are permitted.

You can use the routine BLAS1$VxSWAP to invert the storage of elements of a vector within itself. If incx is greater than 0, then x_i can be moved from location

x(1+(i-1)*incx) to x(1+(n-i)*incx)

The following code fragment inverts the storage of elements of a vector within itself:

NN = N/2 
LHALF = 1+(N-NN)*INCX 
CALL BLAS1$VxSWAP(NN,X,INCX,X(LHALF),-INCX)

BLAS1$VxSWAP does not check for a reserved operand.

Example

C 
C To swap the contents of vectors x and y: 
C 
        INTEGER INCX,INCY,N 
        REAL X(20),Y(20) 
        INCX = 1 
        INCY = 1 
        N = 20 
        CALL BLAS1$VSSWAP(N,X,INCX,Y,INCY) 
C 
C To invert the order of storage of the elements of x within 
C itself; that is, to move x(1),...,x(100) to x(100),...,x(1): 
C 
        INCX = 1 
        INCY = -1 
        N = 50 
        CALL BLAS1$VSSWAP(N,X,INCX,X(51),INCY)

MTH$VxFOLRy_MA_V15

MTH$VxFOLRy_MA_V15 — First Order Linear Recurrence — Multiplication and Addition. The First Order Linear Recurrence — Multiplication and Addition routine provides a vectorized algorithm for the linear recurrence relation that includes both multiplication and addition operations.

Format

MTH$VJFOLRP_MA_V15 n,a,inca,b,incb,c,incc

MTH$VFFOLRP_MA_V15 n,a,inca,b,incb,c,incc

MTH$VDFOLRP_MA_V15 n,a,inca,b,incb,c,incc

MTH$VGFOLRP_MA_V15 n,a,inca,b,incb,c,incc

MTH$VJFOLRN_MA_V15 n,a,inca,b,incb,c,incc

MTH$VFFOLRN_MA_V15 n,a,inca,b,incb,c,incc

MTH$VDFOLRN_MA_V15 n,a,inca,b,incb,c,incc

MTH$VGFOLRN_MA_V15 n,a,inca,b,incb,c,incc

To obtain one of the preceding formats, substitute the following for x and y in MTH$VxFOLRy_MA_V15:

x = J for longword integer, F for F-floating, D for D-floating, G for G-floating

y = P for a positive recursion element, N for a negative recursion element

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Length of the linear recurrence. The n argument is the address of a signed longword integer containing the length.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|inca|

where:

n = length of the linear recurrence specified in n

inca = increment argument for the array a specified in inca

The a argument is the address of a longword integer or floating-point that is this array.

inca

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array a. The inca argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for inca.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|incb|

where:

n = length of the linear recurrence specified in n

incb = increment argument for the array b specified in incb

The b argument is the address of a longword integer or floating-point number that is this array.

incb

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array b. The incb argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for incb.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	modify
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|incc|

where:

n = length of the linear recurrence specified in n

incc = increment argument for the array b specified in incc

The c argument is the address of a longword integer or floating-point number that is this array.

incc

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array c. The incc argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for incc. Do not specify 0 for incc.

Description

MTH$VxFOLRy_MA_V15 is a group of routines that provides a vectorized algorithm for computing the following linear recurrence relation:

C(I+1) = +/-C(I) * A(I) + B(I)

Note

Save the contents of vector registers V0 through V15 before you call this routine.

Call this routine to utilize vector hardware when computing the recurrence. As an example, the call from VSI Fortran is as follows:

K1 = .... 
K2 = .... 
K3 = .... 
CALL MTH$VxFOLRy_MA_V15(N,A(K1),INCA,B(K2),INCB,C(K3),INCC)

The preceding Fortran call replaces the following loop:

K1 = .... 
K2 = .... 
K3 = .... 
DO I = 1, N 
C(K3+I*INCC) = {+/-}C(K3+(I-1)*INCC) * A(K1+(I-1)*INCA) 
               + B(K2+(I-1)*INCB) 
ENDDO

The arrays used in a FOLR expression must be of the same data type in order to be vectorized and user callable. The MTH$ FOLR routines assume that all of the arrays are of the same data type.

This group of routines, MTH$VxFOLRy_MA_V15 (and also MTH$VxFOLRy_z_V8) save the result of each iteration of the linear recurrence relation in an array. This is different from the behavior of MTH$VxFOLRLy_MA_V5 and MTH$VxFOLRLy_z_V2, which return only the result of the last iteration of the linear recurrence relation.

For the output array (c), the increment argument (incc) cannot be 0. However, you can specify 0 for the input increment arguments (inca and incb). In that case, the input will be treated as a scalar value and broadcast to a vector input with all vector elements equal to the scalar value.

In MTH$VxFOLRy_MA_V15, array c can overlap array a and array b, or both, as long as the address of array element c_x is not also the address of an element of a or b that will be referenced at a future time in the recurrence relation. For example, in the following code fragment you must ensure that the address of c(1+i*incc) does not equal the address of either a(j*inca) or b(k*incb) for:

1≤i≤n and j≥i+1.

DO I = 1,N 
C(1+I*INCC) = C(1+(I-1)*INCC) * A(1+(I-1)*INCA) + B(1+(I-1)*INCB) 
ENDDO

Example

C    
C    The following Fortran loop computes a linear recurrence. 
C      
     INTEGER I 
     DIMENSION A(200), B(50), C(50) 
     EQUIVALENCE (B,C) 
     : 
     C(4) = .... 
     DO I = 5, 50 
     C(I) = C((I-1)) * A(I*3) + B(I) 
     ENDDO 
C      
C    This call from Fortran to a FOLR  routine replaces the preceding loop. 
C      
     DIMENSION A(200), B(50), C(50) 
     EQUIVALENCE (B,C) 
     : 
     C(4) = .... 
     CALL MTH$VFFOLRP_MA_V15(46, A(15), 3, B(5), 1, C(4), 1)

C    
C    The following Fortran loop computes a linear recurrence. 
C      
     INTEGER K,N,INCA,INCB,INCC,I 
     DIMENSION A(30), B(6), C(50) 
     K = 44 
     N = 6     
     INCA = 5 
     INCB = 1 
     INCC = 1 
     DO I = 1, N 
     C(K+I*INCC) = -C(K+(I-1)*INCC) * A(I*INCA) + B(I*INCB) 
     ENDDO 
C      
C    This call from Fortran to a FOLR  routine replaces the preceding loop. 
C      
     INTEGER K,N,INCA,INCB,INCC 
     DIMENSION A(30), B(6), C(50) 
     K = 44 
     N = 6 
     INCA = 5 
     INCB = 1 
     INCC = 1 
     CALL MTH$VFFOLRN_MA_V15(N, A(INCA), INCA, B(INCB), INCB, C(K), INCC)

MTH$VxFOLRy_z_V8

MTH$VxFOLRy_z_V8 — First Order Linear Recurrence — Multiplication or Addition. The First Order Linear Recurrence — Multiplication or Addition routine provides a vectorized algorithm for the linear recurrence relation that includes either a multiplication or an addition operation, but not both.

Format

MTH$VJFOLRP_M_V8 n,a,inca,b,incb

MTH$VFFOLRP_M_V8 n,a,inca,b,incb

MTH$VDFOLRP_M_V8 n,a,inca,b,incb

MTH$VGFOLRP_M_V8 n,a,inca,b,incb

MTH$VJFOLRN_M_V8 n,a,inca,b,incb

MTH$VFFOLRN_M_V8 n,a,inca,b,incb

MTH$VDFOLRN_M_V8 n,a,inca,b,incb

MTH$VGFOLRN_M_V8 n,a,inca,b,incb

MTH$VJFOLRP_A_V8 n,a,inca,b,incb

MTH$VFFOLRP_A_V8 n,a,inca,b,incb

MTH$VDFOLRP_A_V8 n,a,inca,b,incb

MTH$VGFOLRP_A_V8 n,a,inca,b,incb

MTH$VJFOLRN_A_V8 n,a,inca,b,incb

MTH$VFFOLRN_A_V8 n,a,inca,b,incb

MTH$VDFOLRN_A_V8 n,a,inca,b,incb

MTH$VGFOLRN_A_V8 n,a,inca,b,incb

To obtain one of the preceding formats, substitute the following for x, y, and z in MTH$VxFOLRy_z_V8:

x = J for longword integer, F for F-floating, D for D-floating, G for G-floating

y = P for a positive recursion element, N for a negative recursion element

z = M for multiplication, A for addition

Returns

None.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Length of the linear recurrence. The n argument is the address of a signed longword integer containing the length.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|inca|

where:

n = length of the linear recurrence specified in n

inca = increment argument for the array a specified in inca

The a argument is the address of a longword integer or floating-point that is this array.

inca

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array a. The inca argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for inca.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|incb|

where:

n = length of the linear recurrence specified in n

incb = increment argument for the array b specified in incb

The b argument is the address of a longword integer or floating-point number that is this array.

incb

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array b. The incb argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for incb.

Description

MTH$VxFOLRy_z_V8 is a group of routines that provide a vectorized algorithm for computing one of the following linear recurrence relations:

B(I) = +/-B(I-1) * A(I)

B(I) = +/-B(I-1) + A(I)

Note

Save the contents of vector registers V0 through V8 before you call this routine.

Call this routine to utilize vector hardware when computing the recurrence. As an example, the call from VSI Fortran is as follows:

CALL MTH$VxFOLRy_z_V8(N,A(K1),INCA,B(K2),INCB)

The preceding Fortran call replaces the following loop:

K1 = .... 
K2 = .... 
DO I = 1, N 
B(K2+I*INCB) = {+/-}B(K2+(I-1)*INCB) {+/*} A(K1+(I-1)*INCA) 
ENDDO

The arrays used in a FOLR expression must be of the same data type in order to be vectorized and user callable. The MTH$ FOLR routines assume that all of the arrays are of the same data type.

This group of routines, MTH$VxFOLRy_z_V8 (and also MTH$VxFOLRy_MA_ V15) save the result of each iteration of the linear recurrence relation in an array. This is different from the behavior of MTH$VxFOLRLy_MA_V5 and MTH$VxFOLRLy_z_V2, which return only the result of the last iteration of the linear recurrence relation.

For the output array (b), the increment argument (incb) cannot be 0. However, you can specify 0 for the input increment argument (inca). In that case, the input will be treated as a scalar and broadcast to a vector input with all vector elements equal to the scalar value.

Example

C 
C    The following Fortran loop computes 
C    a linear recurrence. 
C 
C    D_FLOAT 
     INTEGER N,INCA,INCB,I 
     DIMENSION A(30), B(13) 
     N = 6 
     INCA = 5 
     INCB = 2 
     DO I = 1, N 
     B(1+I*INCB) = -B(1+(I-1)*INCB) * A(I*INCA) 
     ENDDO 
 
C 
C    The following call from Fortran to a FOLR 
C    routine replaces the preceding loop. 
C 
C    D_FLOAT 
     INTEGER N,INCA,INCB 
     REAL*8 A(30), B(13) 
     N = 6 
     INCA = 5 
     INCB = 2 
     CALL MTH$VDFOLRN_M_V8(N, A(INCA), INCA, B(1), INCB)

C    
C    The following Fortran loop computes 
C    a linear recurrence. 
C      
C    G_FLOAT 
     INTEGER N,INCA,INCB 
     DIMENSION A(30), B(13) 
     N = 5 
     INCA = 5 
     INCB = 2 
     DO I = 2, N 
     B(1+I*INCB) = B((I-1)*INCB) + A(I*INCA) 
     ENDDO 
 
C      
C    The following call from Fortran to a FOLR 
C    routine replaces the preceding loop. 
C      
C    G_FLOAT 
     INTEGER N,INCA,INCB 
     REAL*8 A(30), B(13) 
     N = 5 
     INCA = 5 
     INCB = 2 
     CALL MTH$VGFOLRP_A_V8(N, A(INCA), INCA, B(INCB), INCB)

MTH$VxFOLRLy_MA_V5

MTH$VxFOLRLy_MA_V5 — First Order Linear Recurrence — Multiplication and Addition — Last Value. The First Order Linear Recurrence — Multiplication and Addition — Last Value routine provides a vectorized algorithm for the linear recurrence relation that includes both multiplication and addition operations. Only the last value computed is stored.

Format

MTH$VJFOLRLP_MA_V5 n,a,inca,b,incb,t

MTH$VFFOLRLP_MA_V5 n,a,inca,b,incb,t

MTH$VDFOLRLP_MA_V5 n,a,inca,b,incb,t

MTH$VGFOLRLP_MA_V5 n,a,inca,b,incb,t

MTH$VJFOLRLN_MA_V5 n,a,inca,b,incb,t

MTH$VFFOLRLN_MA_V5 n,a,inca,b,incb,t

MTH$VDFOLRLN_MA_V5 n,a,inca,b,incb,t

MTH$VGFOLRLN_MA_V5 n,a,inca,b,incb,t

To obtain one of the preceding formats, substitute the following for x and y in MTH$VxFOLRLy_MA_V5:

x = J for longword integer, F for F-floating, D for D-floating, G for G-floating

y = P for a positive recursion element, N for a negative recursion element

Returns

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating or G_floating
access:	write only
mechanism:	by value

The function value is the result of the last iteration of the linear recurrence relation. The function value is returned in R0 or R0 and R1.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Length of the linear recurrence. The n argument is the address of a signed longword integer containing the length.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|inca|

where:

n = length of the linear recurrence specified in n

inca = increment argument for the array a specified in inca

The a argument is the address of a longword integer or floating-point that is this array.

inca

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array a. The inca argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for inca.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|incb|

where:

n = length of the linear recurrence specified in n

incb = increment argument for the array b specified in incb

The b argument is the address of a longword integer or floating-point number that is this array.

incb

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array b. The incb argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for incb.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	modify
mechanism:	by reference

Variable containing the starting value for the recurrence; overwritten with the value computed by the last iteration of the linear recurrence relation. The t argument is the address of a longword integer or floating-point number that is this value.

Description

MTH$VxFOLRLy_MA_V5 is a group of routines that provide a vectorized algorithm for computing the following linear recurrence relation. (The T on the right side of the equation is the result of the previous iteration of the loop.)

T = +/-T * A(I) + B(I)

Note

Save the contents of vector registers V0 through V5 before you call this routine.

Call this routine to utilize vector hardware when computing the recurrence. As an example, the call from VSI Fortran is as follows:

CALL MTH$VxFOLRy_MA_V5(N,A(K1),INCA,B(K2),INCB,T)

The preceding Fortran call replaces the following loop:

K1 = ... 
K2 = ... 
DO I = 1, N 
T = {+/-}T * A(K1+(I-1)*INCA) + B(K1+(I-1)*INCB) 
ENDDO

The arrays used in a FOLR expression must be of the same data type in order to be vectorized and user callable. The MTH$ FOLR routines assume that all of the arrays are of the same data type.

This group of routines, MTH$VxFOLRLy_MA_V5 (and also MTH$VxFOLRLy_z_V2) returns only the result of the last iteration of the linear recurrence relation. This is different from the behavior of MTH$VxFOLRy_MA_V15 (and also MTH$VxFOLRy_z_V8), which save the result of each iteration of the linear recurrence relation in an array.

If you specify 0 for the input increment arguments (inca and incb), the input will be treated as a scalar and broadcast to a vector input with all vector elements equal to the scalar value.

Example

C    
C    The following Fortran loop computes 
C    a linear recurrence. 
C      
C    G_FLOAT 
     INTEGER N,INCA,INCB,I 
     REAL*8 A(30), B(6), T 
     N = 6 
     INCA = 5 
     INCB = 1 
     T = 78.9847562 
     DO I = 1, N 
     T = -T * A(I*INCA) + B(I*INCB) 
     ENDDO 
 
C      
C    The following call from Fortran to a FOLR 
C    routine replaces the preceding loop. 
C      
C    G_FLOAT 
     INTEGER N,INCA,INCB 
     DIMENSION A(30), B(6), T 
     N = 6 
     INCA = 5 
     INCB = 1 
     T = 78.9847562 
     T = MTH$VGFOLRLN_MA_V5(N, A(INCA), INCA, B(INCB), INCB, T)

C    
C    The following Fortran loop computes 
C    a linear recurrence. 
C      
C    G_FLOAT 
     INTEGER N,INCA,INCB,I 
     REAL*8 A(30), B(6), T 
     N = 6 
     INCA = 5 
     INCB = 1 
     T = 78.9847562 
     DO I = 1, N 
     T = T * A(I*INCA) + B(I*INCB) 
     ENDDO 
 
C      
C    The following call from Fortran to a FOLR 
C    routine replaces the preceding loop. 
C      
C    G_FLOAT 
     INTEGER N,INCA,INCB 
     DIMENSION A(30), B(6), T 
     N = 6 
     INCA = 5 
     INCB = 1 
     T = 78.9847562 
     T = MTH$VGFOLRLP_MA_V5(N, A(INCA), INCA, B(INCB), INCB, T)

MTH$VxFOLRLy_MA_V5

MTH$VxFOLRLy_MA_V5 — First Order Linear Recurrence — Multiplication or Addition — Last Value. The First Order Linear Recurrence — Multiplication or Addition — Last Value routine provides a vectorized algorithm for the linear recurrence relation that includes either a multiplication or an addition operation. Only the last value computed is stored.

Format

MTH$VJFOLRLP_M_V2 n,a,inca,t

MTH$VFFOLRLP_M_V2 n,a,inca,t

MTH$VDFOLRLP_M_V2 n,a,inca,t

MTH$VGFOLRLP_M_V2 n,a,inca,t

MTH$VJFOLRLN_M_V2 n,a,inca,t

MTH$VFFOLRLN_M_V2 n,a,inca,t

MTH$VDFOLRLN_M_V2 n,a,inca,t

MTH$VGFOLRLN_M_V2 n,a,inca,t

MTH$VJFOLRLP_A_V2 n,a,inca,t

MTH$VFFOLRLP_A_V2 n,a,inca,t

MTH$VDFOLRLP_A_V2 n,a,inca,t

MTH$VGFOLRLP_A_V2 n,a,inca,t

MTH$VJFOLRLN_A_V2 n,a,inca,t

MTH$VFFOLRLN_A_V2 n,a,inca,t

MTH$VDFOLRLN_A_V2 n,a,inca,t

MTH$VGFOLRLN_A_V2 n,a,inca,t

To obtain one of the preceding formats, substitute the following for x , y , and z in MTH$VxFOLRLy_z_V2:

x = J for longword integer, F for F-floating, D for D-floating, G for G-floating

y = P for a positive recursion element, N for a negative recursion element

z = M for multiplication, A for addition

Returns

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating or G_floating
access:	write only
mechanism:	by value

The function value is the result of the last iteration of the linear recurrence relation. The function value is returned in R0 or R0 and R1.

Argument

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Length of the linear recurrence. The n argument is the address of a signed longword integer containing the length.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	read only
mechanism:	by reference, array reference

Array of length at least:

1+(n-1)*|inca|

where:

n = length of the linear recurrence specified in n

inca = increment argument for the array a specified in inca

The a argument is the address of a longword integer or floating-point that is this array.

inca

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

Increment argument for the array a. The inca argument is the address of a signed longword integer containing the increment argument. For contiguous elements, specify 1 for inca.

OpenVMS usage:	longword_signed or floating_point
type:	longword integer (signed), F_floating, D_floating, or G_floating
access:	modify
mechanism:	by reference

Description

MTH$VxFOLRLy_z_V2 is a group of routines that provide a vectorized algorithm for computing one of the following linear recurrence relations. (The T on the right side of the following equations is the result of the previous iteration of the loop.)

T = +/-T * A(I)

T = +/-T + A(I)

Note

Save the contents of vector registers V0, V1, and V2 before you call this routine.

Call this routine to utilize vector hardware when computing the recurrence. As an example, the call from VSI Fortran is as follows:

CALL MTH$VxFOLRLy_z_V2(N,A(K1),INCA,T)

The preceding Fortran call replaces the following loop:

K1 = .... 
DO I = 1, N 
T = {+/-}T {+/*} A(K1+(I-1)*INCA) 
ENDDO

The arrays used in a FOLR expression must be of the same data type in order to be vectorized and user callable. The MTH$ FOLR routines assume that all of the arrays are of the same data type.

This group of routines, MTH$VxFOLRLy_z_V2 (and also MTH$VxFOLRLy_MA_V5) return only the result of the last iteration of the linear recurrence relation. This is different from the behavior of MTH$VxFOLRy_MA_V15 (and also MTH$VxFOLRy_z_V8), which save the result of each iteration of the linear recurrence relation in an array.

If you specify 0 for the input increment argument (inca), the input will be treated as a scalar and broadcast to a vector input with all vector elements equal to the scalar value.

Example

C    
C    The following Fortran loop computes 
C    a linear recurrence. 
C      
C    D_FLOAT 
     INTEGER I,N 
     REAL*8 A(200), T 
     T = 78.9847562 
     N = 20 
     DO I = 4, N 
     T = -T * A(I*10) 
     ENDDO 
 
C      
C    The following call from Fortran to a FOLR 
C    routine replaces the preceding loop. 
C      
C    D_FLOAT 
     INTEGER N 
     REAL*8 A(200), T 
     T = 78.9847562 
     N = 20 
     T = MTH$VDFOLRLN_M_V2(N-3, A(40), 10, T)

C    
C    The following Fortran loop computes 
C    a linear recurrence. 
C      
C    D_FLOAT 
     INTEGER I,N 
     REAL*8 A(200), T 
     T = 78.9847562 
     N = 20 
     DO I = 4, N 
     T = T + A(I*10) 
     ENDDO 
 
C      
C    The following call from Fortran to a FOLR 
C    routine replaces the preceding loop. 
C      
C    D_FLOAT 
     INTEGER N 
     REAL*8 A(200), T 
     T = 78.9847562 
     N = 20 
     T = MTH$VDFOLRLP_A_V2(N-3, A(40), 10, T)

Appendix A. Additional MTH$ Routines

The following supported MTH$ routines are not included with the routines in the Scalar MTH$ Reference Section because they are rarely used. The majority of these routines serve to satisfy external references when intrinsic functions in Fortran and other languages are passed as parameters. Otherwise, the functions are performed by inline code.

Table A–1 lists all of the entry point and argument information for the MTH$ routines not documented in the Scalar MTH$ Reference Section of this manual.

Table A.1. Additional MTH$ Routines

Routine Name		Entry Point Information
MTH$ABS		F-floating Absolute Value Routine
	Format:	MTH$ABS f-floating
	Returns:	floating_point, F_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DABS		D-floating Absolute Value Routine
	Format:	MTH$DABS d-floating
	Returns:	floating_point, D_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$GABS		G-floating Absolute Value Routine
	Format:	MTH$GABS g-floating
	Returns:	floating_point, G_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$HABS		H-floating Absolute Value Routine
	Format:	MTH$HABS h-abs-val, h-floating
	Returns:	None
	h-abs-val:	floating_point, H_floating, write only, by reference
	h-floating:	floating_point, H_floating, read only, by reference

MTH$IIABS		Word Absolute Value Routine
	Format:	MTH$IIABS word
	Returns:	word_signed, word (signed), write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$JIABS		Longword Absolute Value Routine
	Format:	MTH$JIABS longword
	Returns:	longword_signed, longword (signed), write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$IIAND		Bitwise AND of Two Word Parameters Routine
	Format:	MTH$IIAND word1, word2
	Returns:	word_unsigned, word (unsigned), write only, by value
	word1:	word_unsigned, word (unsigned), read only, by reference
	word2:	word_unsigned, word (unsigned), read only, by reference

MTH$JIAND		Bitwise AND of Two Longword Parameters Routine
	Format:	MTH$JIAND longword1, longword2
	Returns:	longword_unsigned, longword (unsigned), write only, by value
	longword1:	longword_unsigned, longword (unsigned), read only, by reference
	longword2:	longword_unsigned, longword (unsigned), read only, by reference

MTH$DBLE		Convert F-floating to D-floating (Exact) Routine
	Format:	MTH$DBLE f-floating
	Returns:	floating_point, D_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$GDBLE		Convert F-floating to G-floating (Exact) Routine
	Format:	MTH$GDBLE f-floating
	Returns:	floating_point, G_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DIM		Positive Difference of Two F-floating Parameters Routine
	Format:	MTH$DIM f-floating1, f-floating2
	Returns:	floating_point, F_floating, write only, by value
	f-floating1:	floating_point, F_floating, read only, by reference
	f-floating2:	floating_point, F_floating, read only, by reference

MTH$DDIM		Positive Difference of Two D-floating Parameters Routine
	Format:	MTH$DDIM d-floating1, d-floating2
	Returns:	floating_point, D_floating, write only, by value
	d-floating1:	floating_point, D_floating, read only, by reference
	d-floating2:	floating_point, D_floating, read only, by reference

MTH$GDIM		Positive Difference of Two G-floating Parameters Routine
	Format:	MTH$GDIM g-floating1, g-floating2
	Returns:	floating_point, G_floating, write only, by value
	g-floating1:	floating_point, G_floating, read only, by reference
	g-floating2:	floating_point, G_floating, read only, by reference

MTH$HDIM		Positive Difference of Two H-floating Parameters Routine
	Format:	MTH$HDIM h-floating, h-floating1, h-floating2
	Returns:	None
	h-floating:	floating_point, H_floating, write only, by reference
	h-floating1:	floating_point, H_floating, read only, by reference
	h-floating2:	floating_point, H_floating, read only, by reference

MTH$IIDIM		Positive Difference of Two Word Parameters Routine
	Format:	MTH$IIDIM word1, word2
	Returns:	word_signed, word (signed), write only, by value
	word1:	word_signed, word (signed), read only, by reference
	word2:	word_signed, word (signed), read only, by reference

MTH$JIDIM		Positive Difference of Two Longword Parameters Routine
	Format:	MTH$JIDIM longword1, longword2
	Returns:	longword_signed, longword (signed), write only, by value
	longword1:	longword_signed, longword (signed), read only, by reference
	longword2:	longword_signed, longword (signed), read only, by reference

MTH$IIEOR		Bitwise Exclusive OR of Two Word Parameters Routine
	Format:	MTH$IIEOR word1, word2
	Returns:	word_unsigned, word (unsigned), write only, by value
	word1:	word_unsigned, word (unsigned), read only, by reference
	word2:	word_unsigned, word (unsigned), read only, by reference

MTH$JIEOR		Bitwise Exclusive OR of Two Longword Parameters Routine
	Format:	MTH$JIEOR longword1, longword2
	Returns:	longword_unsigned, longword (unsigned), write only, by value
	longword1:	longword_unsigned, longword (unsigned), read only, by reference
	longword2:	longword_unsigned, longword (unsigned), read only, by reference

MTH$IIFIX		Convert F-floating to Word (Truncated) Routine
	Format:	MTH$IIFIX f-floating
	Returns:	word_signed, word (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$JIFIX		Convert F-floating to Longword (Truncated) Routine
	Format:	MTH$JIFIX f-floating
	Returns:	longword_signed, longword (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$FLOATI		Convert Word to F-floating (Exact) Routine
	Format:	MTH$FLOATI word
	Returns:	floating_point, F_floating, write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$DFLOTI		Convert Word to D-floating (Exact) Routine
	Format:	MTH$DFLOTI word
	Returns:	floating_point, D_floating, write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$GFLOTI		Convert Word to G-floating (Exact) Routine
	Format:	MTH$GFLOTI word
	Returns:	floating_point, G_floating, write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$FLOATJ		Convert Longword to F-floating (Rounded) Routine
	Format:	MTH$FLOATJ longword
	Returns:	floating_point, F_floating, write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$DFLOTJ		Convert Longword to D-floating (Exact) Routine
	Format:	MTH$DFLOTJ longword
	Returns:	floating_point, D_floating, write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$GFLOTJ		Convert Longword to G-floating (Exact) Routine
	Format:	MTH$GFLOTJ longword
	Returns:	floating_point, G_floating, write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$FLOOR		Convert F-floating to Greatest F-floating Integer Routine
	Format:	MTH$FLOOR f-floating
	JSB:	MTH$FLOOR_R1 f-floating
	Returns:	floating_point, F_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DFLOOR		Convert D-floating to Greatest D-floating Integer Routine
	Format:	MTH$DFLOOR d-floating
	JSB:	MTH$DFLOOR_R3 d-floating
	Returns:	floating_point, D_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$GFLOOR		Convert G-floating to Greatest G-floating Integer Routine
	Format:	MTH$GFLOOR g-floating
	JSB:	MTH$GFLOOR_R3 g-floating
	Returns:	floating_point, G_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$HFLOOR		Convert H-floating to Greatest H-floating Integer Routine
	Format:	MTH$HFLOOR max-h-float, h-floating
	JSB:	MTH$HFLOOR_R7 h-floating
	Returns:	None
	max-h-float:	floating_point, H_floating, write only, by reference
	h-floating:	floating_point, H_floating, read only, by reference

MTH$AINT		Convert F-floating to Truncated F-floating Routine
	Format:	MTH$AINT f-floating
	JSB:	MTH$AINT_R2 f-floating
	Returns:	floating_point, F_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DINT		Convert D-floating to Truncated D-floating Routine
	Format:	MTH$DINT d-floating
	JSB:	MTH$DINT_R4 d-floating
	Returns:	floating_point, D_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$IIDINT		Convert D-floating to Word (Truncated) Routine
	Format:	MTH$IIDINT d-floating
	Returns:	word_signed, word (signed), write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$JIDINT		Convert D-floating to Longword (Truncated) Routine
	Format:	MTH$JIDINT d-floating
	Returns:	longword_signed, longword (signed), write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$GINT		Convert G-floating to Truncated G-floating Routine
	Format:	MTH$GINT g-floating
	JSB:	MTH$GINT_R4 g-floating
	Returns:	floating_point, G_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$IIGINT		Convert G-floating to Word (Truncated) Routine
	Format:	MTH$IIGINT g-floating
	Returns:	word_signed, word (signed), write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$JIGINT		Convert G-floating to Longword (Truncated) Routine
	Format:	MTH$JIGINT g-floating
	Returns:	longword_signed, longword (signed), write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$HINT		Convert H-floating to Truncated H-floating Routine
	Format:	MTH$HINT trunc-h-flt, h-floating
	JSB:	MTH$HINT_R8 h-floating
	Returns:	None
	trunc-h-flt:	floating_point, H_floating, write only, by reference
	h-floating:	floating_point, H_floating, read only, by reference

MTH$IIHINT		Convert H-floating to Word (Truncated) Routine
	Format:	MTH$IIHINT h-floating
	Returns:	word_signed, word (signed), write only, by value
	h-floating:	floating_point, H_floating, read only, by reference

MTH$JIHINT		Convert H-floating to Longword (Truncated) Routine
	Format:	MTH$JIHINT h-floating
	Returns:	longword_signed, longword (signed), write only, by value
	h-floating:	floating_point, H_floating, read only, by reference

MTH$IINT		Convert F-floating to Word (Truncated) Routine
	Format:	MTH$IINT f-floating
	Returns:	word_signed, word (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$JINT		Convert F-floating to Longword (Truncated) Routine
	Format:	MTH$JINT f-floating
	Returns:	longword_signed, longword (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$IIOR		Bitwise Inclusive OR of Two Word Parameters Routine
	Format:	MTH$IIOR word1, word2
	Returns:	word_unsigned, word (unsigned), write only, by value
	word1:	word_unsigned, word (unsigned), read only, by reference
	word2:	word_unsigned, word (unsigned), read only, by reference

MTH$JIOR		Bitwise Inclusive OR of Two Longword Parameters Routine
	Format:	MTH$JIOR longword1, longword2
	Returns:	longword_unsigned, longword (unsigned), write only, by value
	longword1:	longword_unsigned, longword (unsigned), read only, by reference
	longword2:	longword_unsigned, longword (unsigned), read only, by reference

MTH$AIMAX0		F-floating Maximum of N Word Parameters Routine
	Format:	MTH$AIMAX0 word, ...
	Returns:	floating_point, F_floating, write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$AJMAX0		F-floating Maximum of N Longword Parameters Routine
	Format:	MTH$AJMAX0 longword, ...
	Returns:	floating_point, F_floating, write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$IMAX0		Word Maximum of N Word Parameters Routine
	Format:	MTH$IMAX0 word, ...
	Returns:	word_signed, word (signed), write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$JMAX0		Longword Maximum of N Longword Parameters Routine
	Format:	MTH$JMAX0 longword, ...
	Returns:	longword_signed, longword (signed), write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$AMAX1		F-floating Maximum of N F-floating Parameters Routine
	Format:	MTH$AMAX1 f-floating, ...
	Returns:	floating_point, F_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DMAX1		D-floating Maximum of N D-floating Parameters Routine
	Format:	MTH$DMAX1 d-floating, ...
	Returns:	floating_point, D_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$GMAX1		G-floating Maximum of N G-floating Parameters Routine
	Format:	MTH$GMAX1 g-floating, ...
	Returns:	floating_point, G_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$HMAX1		H-floating Maximum of N H-floating Parameters Routine
	Format:	MTH$HMAX1 h-float-max, h-floating, ...
	Returns:	None
	h-float-max:	floating_point, H_floating, write only, by reference
	h-floating:	floating_point, H_floating, read only, by reference

MTH$IMAX1		Word Maximum of N F-floating Parameters Routine
	Format:	MTH$IMAX1 f-floating, ...
	Returns:	word_signed, word (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$JMAX1		Longword Maximum of N F-floating Parameters Routine
	Format:	MTH$JMAX1 f-floating, ...
	Returns:	longword_signed, longword (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$AIMIN0		F-floating Minimum of N Word Parameters Routine
	Format:	MTH$AIMIN0 word, ...
	Returns:	floating_point, F_floating, write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$AJMIN0		F-floating Minimum of N Longword Parameters Routine
	Format:	MTH$AJMIN0 longword, ...
	Returns:	floating_point, F_floating, write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$IMIN0		Word Minimum of N Word Parameters Routine
	Format:	MTH$IMIN0 word, ...
	Returns:	word_signed, word (signed), write only, by value
	word:	word_signed, word (signed), read only, by reference

MTH$JMIN0		Longword Minimum of N Longword Parameters Routine
	Format:	MTH$JMIN0 longword, ...
	Returns:	longword_signed, longword (signed), write only, by value
	longword:	longword_signed, longword (signed), read only, by reference

MTH$AMIN1		F-floating Minimum of N F-floating Parameters Routine
	Format:	MTH$AMIN1 f-floating, ...
	Returns:	floating_point, F_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DMIN1		D-floating Minimum of N D-floating Parameters Routine
	Format:	MTH$DMIN1 d-floating, ...
	Returns:	floating_point, D_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$GMIN1		G-floating Minimum of N G-floating Parameters Routine
	Format:	MTH$GMIN1 g-floating, ...
	Returns:	floating_point, G_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$HMIN1		H-floating Minimum of N H-floating Parameters Routine
	Format:	MTH$HMIN1 h-float-max, h-floating, ...
	Returns:	None
	h-float-max:	floating_point, H_floating, write only, by reference
	h-floating:	floating_point, H_floating, read only, by reference

MTH$IMIN1		Word Minimum of N F-floating Parameters Routine
	Format:	MTH$IMIN1 f-floating, ...
	Returns:	word_signed, word (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$JMIN1		Longword Minimum of N F-floating Parameters Routine
	Format:	MTH$JMIN1 f-floating, ...
	Returns:	longword_signed, longword (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$AMOD		Remainder from Division of Two F-floating Parameters Routine
	Format:	MTH$AMOD dividend, divisor
	Returns:	floating_point, F_floating, write only, by value
	dividend:	floating_point, F_floating, read only, by reference
	divisor:	floating_point, F_floating, read only, by reference

MTH$DMOD		Remainder from Division of Two D-floating Parameters Routine
	Format:	MTH$DMOD dividend, divisor
	Returns:	floating_point, D_floating, write only, by value
	dividend:	floating_point, D_floating, read only, by reference
	divisor:	floating_point, D_floating, read only, by reference

MTH$GMOD		Remainder from Division of Two G-floating Parameters Routine
	Format:	MTH$GMOD dividend, divisor
	Returns:	floating_point, G_floating, write only, by value
	dividend:	floating_point, G_floating, read only, by reference
	divisor:	floating_point, G_floating, read only, by reference

MTH$HMOD		Remainder from Division of Two H-floating Parameters Routine
	Format:	MTH$HMOD h-mod, dividend, divisor
	Returns:	None
	h-mod:	floating_point, H_floating, write only, by reference
	dividend:	floating_point, H_floating, read only, by reference
	divisor:	floating_point, H_floating, read only, by reference

MTH$IMOD		Remainder from Division of Two Word Parameters Routine
	Format:	MTH$IMOD dividend, divisor
	Returns:	word_signed, word (signed), write only, by value
	dividend:	word_signed, word (signed), read only, by reference
	divisor:	word_signed, word (signed), read only, by reference

MTH$JMOD		Remainder of Two Longword Parameters Routine
	Format:	MTH$JMOD dividend, divisor
	Returns:	longword_signed, longword (signed), write only, by value
	dividend:	longword_signed, longword (signed), read only, by reference
	divisor:	longword_signed, longword (signed), read only, by reference

MTH$ANINT		Convert F-floating to Nearest F-floating Integer Routine
	Format:	MTH$ANINT f-floating
	Returns:	floating_point, F_floating, write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$DNINT		Convert D-floating to Nearest D-floating Integer Routine
	Format:	MTH$DNINT d-floating
	Returns:	floating_point, D_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$IIDNNT		Convert D-floating to Nearest Word Integer Routine
	Format:	MTH$IIDNNT d-floating
	Returns:	word_signed, word (signed), write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$JIDNNT		Convert D-floating to Nearest Longword Integer Routine
	Format:	MTH$JIDNNT d-floating
	Returns:	longword_signed, longword (signed), write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$GNINT		Convert G-floating to Nearest G-floating Integer Routine
	Format:	MTH$GNINT g-floating
	Returns:	floating_point, G_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$IIGNNT		Convert G-floating to Nearest Word Integer Routine
	Format:	MTH$IIGNNT g-floating
	Returns:	word_signed, word (signed), write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$JIGNNT		Convert G-floating to Nearest Longword Integer Routine
	Format:	MTH$JIGNNT g-floating
	Returns:	longword_signed, longword (signed), write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

MTH$HNINT		Convert H-floating to Nearest H-floating Integer Routine
	Format:	MTH$HNINT nearst-h-flt, h-floating
	Returns:	None
	nearst-h-flt:	floating_point, H_floating, write only, by reference
	h-floating:	floating_point, H_floating, read only, by reference

MTH$IIHNNT		Convert H-floating to Nearest Word Integer Routine
	Format:	MTH$IIHNNT h-floating
	Returns:	word_signed, word (signed), write only, by value
	h-floating:	floating_point, H_floating, read only, by reference

MTH$JIHNNT		Convert H-floating to Nearest Longword Integer Routine
	Format:	MTH$JIHNNT h-floating
	Returns:	longword_signed, longword (signed), write only, by value
	h-floating:	floating_point, H_floating, read only, by reference

MTH$ININT		Convert F-floating to Nearest Word Integer Routine
	Format:	MTH$ININT f-floating
	Returns:	word_signed, word (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$JNINT		Convert F-floating to Nearest Longword Integer Routine
	Format:	MTH$JNINT f-floating
	Returns:	longword_signed, longword (signed), write only, by value
	f-floating:	floating_point, F_floating, read only, by reference

MTH$INOT		Bitwise Complement of Word Parameter Routine
	Format:	MTH$INOT word
	Returns:	word_unsigned, word (unsigned), write only, by value
	word:	word_unsigned, word (unsigned), read only, by reference

MTH$JNOT		Bitwise Complement of Longword Parameter Routine
	Format:	MTH$JNOT longword
	Returns:	longword_unsigned, longword (unsigned), write only, by value
	longword:	longword_unsigned, longword (unsigned), read only, by reference

MTH$DPROD		D-floating Product of Two F-floating Parameters Routine
	Format:	MTH$DPROD f-floating1, f-floating2
	Returns:	floating_point, D_floating, write only, by value
	f-floating1:	floating_point, F_floating, read only, by reference
	f-floating2:	floating_point, F_floating, read only, by reference

MTH$GPROD		G-floating Product of Two F-floating Parameters Routine
	Format:	MTH$GPROD f-floating1, f-floating2
	Returns:	floating_point, G_floating, write only, by value
	f-floating1:	floating_point, F_floating, read only, by reference
	f-floating2:	floating_point, F_floating, read only, by reference

MTH$SGN		F-floating Sign Function
	Format:	MTH$SGN f-floating
	Returns:	longword_signed, longword (signed), write only, by reference
	f-floating:	floating_point, F_floating, read only, by reference

MTH$SGN		D-floating Sign Function
	Format:	MTH$SGN d-floating
	Returns:	longword_signed, longword (signed), write only, by reference
	d-floating:	floating_point, D_floating, read only, by reference

MTH$IISHFT		Bitwise Shift of Word Routine
	Format:	MTH$IISHFT word, shift-cnt
	Returns:	word_unsigned, word (unsigned), write only, by value
	word:	word_unsigned, word (unsigned), read only, by reference
	shift-cnt:	word_signed, word (signed), read only, by reference

MTH$JISHFT		Bitwise Shift of Longword Routine
	Format:	MTH$JISHFT longword, shift-cnt
	Returns:	longword_unsigned, longword (unsigned), write only, by value
	longword:	longword_unsigned, longword (unsigned), read only, by reference
	shift-cnt:	longword_signed, longword (signed), read only, by reference

MTH$SIGN		F-floating Transfer of Sign of Y to Sign of X Routine
	Format:	MTH$SIGN f-float-x, f-float-y
	Returns:	floating_point, F_floating, write only, by value
	f-float-x:	floating_point, F_floating, read only, by reference
	f-float-y:	floating_point, F_floating, read only, by reference

MTH$DSIGN		D-floating Transfer of Sign of Y to Sign of X Routine
	Format:	MTH$DSIGN d-float-x, d-float-y
	Returns:	floating_point, D_floating, write only, by value
	d-float-x:	floating_point, D_floating, read only, by reference
	d-float-y:	floating_point, D_floating, read only, by reference

MTH$GSIGN		G-floating Transfer of Sign of Y to Sign of X Routine
	Format:	MTH$GSIGN g-float-x, g-float-y
	Returns:	floating_point, G_floating, write only, by value
	g-float-x:	floating_point, G_floating, read only, by reference
	g-float-y:	floating_point, G_floating, read only, by reference

MTH$HSIGN		H-floating Transfer of Sign of Y to Sign of X Routine
	Format:	MTH$HSIGN h-result, h-float-x, h-float-y
	Returns:	None
	h-result:	floating_point, H_floating, write only, by reference
	h-float-x:	floating_point, H_floating, read only, by reference
	h-float-y:	floating_point, H_floating, read only, by reference

MTH$IISIGN		Word Transfer of Sign of Y to Sign of X Routine
	Format:	MTH$IISIGN word-x, word-y
	Returns:	word_signed, word (signed), write only, by value
	word-x:	word_signed, word (signed), read only, by reference
	word-y:	word_signed, word (signed), read only, by reference

MTH$JISIGN		Longword Transfer of Sign of Y to Sign of X Routine
	Format:	MTH$JISIGN longwrd-x, longwrd-y
	Returns:	longword_signed, longword (signed), write only, by reference
	longwrd-x:	longword_signed, longword (signed), read only, by reference
	longwrd-y:	longword_signed, longword (signed), read only, by reference

MTH$SNGL		Convert D-floating to F-floating (Rounded) Routine
	Format:	MTH$SNGL d-floating
	Returns:	floating_point, F_floating, write only, by value
	d-floating:	floating_point, D_floating, read only, by reference

MTH$SNGLG		Convert G-floating to F-floating (Rounded) Routine
	Format:	MTH$SNGLG g-floating
	Returns:	floating_point, F_floating, write only, by value
	g-floating:	floating_point, G_floating, read only, by reference

Appendix B. Vector MTH$ Routine Entry Points

Table B–1 contains all of the vector MTH$ routines that you can call from VAX MACRO. Be sure to read Section 2.3.3 and Section 2.3.4 before using the information in this table.

Table B.1. Vector MTH$ Routines

Scalar Name	Call or JSB	Vector Input Registers	Vector Output Registers	Vector Name (Underflows Not Signaled)	Vector Name (Underflows Signaled)
AINT	JSB	V0	V0	MTH$VAINT_R0_V1
DINT	JSB	V0	V0	MTH$VDINT_R3_V3
GINT	JSB	V0	V0	MTH$VGINT_R3_V3
DPROD	Call	V0,V1	V0	MTH$VVDPROD_R1_V1
GPROD	Call	V0,V1	V0	MTH$VVGPROD_R1_V1
ACOS	JSB	V0	V0	MTH$VACOS_R6_V7
DACOS	JSB	V0	V0	MTH$VDACOS_R2_V7
GACOS	JSB	V0	V0	MTH$VGACOS_R2_V7
ACOSD	JSB	V0	V0	MTH$VACOSD_R6_V7
DACOSD	JSB	V0	V0	MTH$VDACOSD_R2_V7
GACOSD	JSB	V0	V0	MTH$VGACOS_R2_V7
ASIN	JSB	V0	V0	MTH$VASIN_R2_V6
DASIN	JSB	V0	V0	MTH$VDASIN_R2_V6
GASIN	JSB	V0	V0	MTH$VGASIN_R2_V6
ASIND	JSB	V0	V0	MTH$VASIND_R2_V6
DASIND	JSB	V0	V0	MTH$VDASIND_R2_V6
GASIND	JSB	V0	V0	MTH$VGASIND_R2_V6
ATAN	JSB	V0	V0	MTH$VATAN_R0_V4
DATAN	JSB	V0	V0	MTH$VDATAN_R0_V6
GATAN	JSB	V0	V0	MTH$VGATAN_R0_V6
ATAND	JSB	V0	V0	MTH$VATAND_R0_V4
DATAND	JSB	V0	V0	MTH$VDATAND_R0_V6
GATAND	JSB	V0	V0	MTH$VGATAND_R0_V6
ATAN2	JSB	V0,V1	V0	MTH$VVATAN2_R4_V7
DATAN2	JSB	V0,V1	V0	MTH$VVDATAN2_R4_V9
GATAN2	JSB	V0,V1	V0	MTH$VVGATAN2_R4_V9
ATAND2	JSB	V0,V1	V0	MTH$VVATAND2_R4_V7
DATAND2	JSB	V0,V1	V0	MTH$VVDATAND2_R4_V9
GATAND2	JSB	V0,V1	V0	MTH$VVGATAND2_R4_V9
CABS	Call	V0,V1	V0	MTH$VCABS_R1_V5
CDABS	Call	V0,V1	V0	MTH$VCDABS_R1_V6
CGABS	Call	V0,V1	V0	MTH$VCGABS_R1_V6
CCOS	Call	V0,V1	V0,V1	MTH$VCCOS_R1_V11
CDCOS	Call	V0,V1	V0,V1	MTH$VCDCOS_R1_V11
CGCOS	Call	V0,V1	V0,V1	MTH$VCGCOS_R1_V11
COS	JSB	V0	V0	MTH$VCOS_R4_V7
DCOS	JSB	V0	V0	MTH$VDCOS_R4_V8
GCOS	JSB	V0	V0	MTH$VGCOS_R4_V8
COSD	JSB	V0	V0	MTH$VCOSD_R4_V6
DCOSD	JSB	V0	V0	MTH$VDCOSD_R4_V6
GCOSD	JSB	V0	V0	MTH$VGCOSD_R4_V6
CEXP	Call	V0,V1	V0,V1	MTH$VCEXP_R1_V8
CDEXP	Call	V0,V1	V0,V1	MTH$VCDEXP_R1_V10
CGEXP	Call	V0,V1	V0,V1	MTH$VCGEXP_R1_V10
CLOG	Call	V0,V1	V0,V1	MTH$VCLOG_R1_V8
CDLOG	Call	V0,V1	V0,V1	MTH$VCDLOG_R1_V10
CGLOG	Call	V0,V1	V0,V1	MTH$VCGLOG_R1_V10
AMOD	JSB	V0,R0	V0	MTH$VAMOD_R4_V5	MTH$VAMOD_E_R4_V5
DMOD	JSB	V0,R0	V0	MTH$VDMOD_R7_V6	MTH$VDMOD_E_R7_V6
GMOD	JSB	V0,R0	V0	MTH$VGMOD_R7_V6	MTH$VGMOD_E_R7_V6
CSIN	Call	V0,V1	V0,V1	MTH$VCSIN_R1_V11
CDSIN	Call	V0,V1	V0,V1	MTH$VCDSIN_R1_V11
CGSIN	Call	V0,V1	V0,V1	MTH$VCGSIN_R1_V11
CSQRT	Call	V0,V1	V0,V1	MTH$VCSQRT_R1_V7
CDSQRT	Call	V0,V1	V0,V1	MTH$VCDSQRT_R1_V8
CGSQRT	Call	V0,V1	V0,V1	MTH$VCGSQRT_R1_V8
COSH	JSB	V0	V0	MTH$VCOSH_R5_V8
DCOSH	JSB	V0	V0	MTH$VDCOSH_R5_V8
GCOSH	JSB	V0	V0	MTH$VGCOSH_R5_V8
EXP	JSB	V0	V0	MTH$VEXP_R3_V6	MTH$VEXP_E_R3_V6
DEXP	JSB	V0	V0	MTH$VDEXP_R3_V6	MTH$VDEXP_E_R3_V6
GEXP	JSB	V0	V0	MTH$VGEXP_R3_V6	MTH$VGEXP_E_R3_V6
ALOG	JSB	V0	V0	MTH$VALOG_R3_V5
DLOG	JSB	V0	V0	MTH$VDLOG_R3_V7
GLOG	JSB	V0	V0	MTH$VGLOG_R3_V7
ALOG10	JSB	V0	V0	MTH$VALOG10_R3_V5
DLOG10	JSB	V0	V0	MTH$VDLOG10_R3_V7
GLOG10	JSB	V0	V0	MTH$VGLOG10_R3_V7
ALOG2	JSB	V0	V0	MTH$VALOG2_R3_V5
DLOG2	JSB	V0	V0	MTH$VDLOG2_R3_V7
GLOG2	JSB	V0	V0	MTH$VGLOG2_R3_V7
RANDOM	JSB	V0	V0	MTH$VRANDOM_R2_V0
SIN	JSB	V0	V0	MTH$VSIN_R4_V6
DSIN	JSB	V0	V0	MTH$VDSIN_R4_V8
GSIN	JSB	V0	V0	MTH$VGSIN_R4_V8
SIND	JSB	V0	V0	MTH$VSIND_R4_V6	MTH$VSIND_E_R6_V6
DSIND	JSB	V0	V0	MTH$VDSIND_R4_V6	MTH$VDSIND_E_R6_V6
GSIND	JSB	V0	V0	MTH$VGSIND_R4_V6	MTH$VGSIND_E_R6_V6
SINCOS	JSB	V0	V0,V1	MTH$VSINCOS_R4_V7
DSINCOS	JSB	V0	V0,V1	MTH$VDSINCOS_R4_V8
GSINCOS	JSB	V0	V0,V1	MTH$VGSINCOS_R4_V8
SINCOSD	JSB	V0	V0,V1	MTH$VSINCOSD_R4_V6	MTH$VSINCOSD_E_R6_V6
DSINCOSD	JSB	V0	V0,V1	MTH$VDSINCOSD_R4_V7	MTH$VDSINCOSD_E_R6_V7
GSINCOSD	JSB	V0	V0,V1	MTH$VGSINCOSD_R4_V7	MTH$VGSINCOSD_E_R6_V7
SINH	JSB	V0	V0	MTH$VSINH_R5_V9
DSINH	JSB	V0	V0	MTH$VDSINH_R5_V9
GSINH	JSB	V0	V0	MTH$VGSINH_R5_V9
SQRT	JSB	V0	V0	MTH$VSQRT_R2_V4
DSQRT	JSB	V0	V0	MTH$VDSQRT_R2_V5
GSQRT	JSB	V0	V0	MTH$VGSQRT_R2_V5
TAN	JSB	V0	V0	MTH$VTAN_R4_V5
DTAN	JSB	V0	V0	MTH$VDTAN_R4_V5
GTAN	JSB	V0	V0	MTH$VGTAN_R4_V5
TAND	JSB	V0	V0	MTH$VTAND_R4_V5	MTH$VTAND_E_R4_V5
DTAND	JSB	V0	V0	MTH$VDTAND_R4_V5	MTH$VDTAND_E_R4_V5
GTAND	JSB	V0	V0	MTH$VGTAND_R4_V5	MTH$VGTAND_E_R4_V5
TANH	JSB	V0	V0	MTH$VTANH_R3_V10
DTANH	JSB	V0	V0	MTH$VDTANH_R3_V10
GTANH	JSB	V0	V0	MTH$VGTANH_R3_V10
DIVC	Call	V0,V1, V2,V3	V0,V1	OTS$VVDIVC_R1_V6
DIVCD	Call	V0,V1, V2,V3	V0,V1	OTS$VVDIVCD_R1_V7
DIVCG	Call	V0,V1, V2,V3	V0,V1	OTS$VVDIVCG_R1_V7
MULC	Call	V0,V1, V2,V3	V0,V1	OTS$VVMULC_R1_V4
MULCD	Call	V0,V1, V2,V3	V0,V1	OTS$VVMULCD_R1_V4
MULCG	Call	V0,V1, V2,V3	V0,V1	OTS$VVMULCG_R1_V4
POWJJ	Call	V0,R0	V0	OTS$VPOWJJ_R1_V1
POWRJ	Call	V0,R0	V0	OTS$VPOWRJ_R1_V2	OTS$VPOWRJ_E_R1_V2
POWDJ	Call	V0,R0	V0	OTS$VPOWDJ_R1_V2	OTS$VPOWDJ_E_R1_V2
POWGJ	Call	V0,R0	V0	OTS$VPOWGJ_R1_V2	OTS$VPOWGJ_E_R1_V2
POWRR	Call	V0,R0	V0	OTS$VPOWRR_R1_V4	OTS$VPOWRR_E_R1_V4
POWDD	Call	V0,R0	V0	OTS$VPOWDD_R1_V8	OTS$VPOWDD_E_R1_V8
POWGG	Call	V0,R0	V0	OTS$VPOWGG_R1_V9	OTS$VPOWGG_E_R1_V9

Value of I	zSIN(X)	zCOS(X)
0	zSIN(Y)	zCOS(Y)
1	zCOS(Y)	zSIN(Y)
2	zCOS(Y)	-zSIN(Y)
3	zSIN(Y)	-zCOS(Y)
4	-zSIN(Y)	-zCOS(Y)
5	-zCOS(Y)	-zSIN(Y)
6	-zCOS(Y)	zSIN(Y)
7	-zSIN(Y)	zCOS(Y)

Value of I	zSIND(X)	zCOSD(X)
0	zSIND(Y)	zCOSD(Y)
1	zCOSD(Y)	zSIND(Y)
2	zCOSD(Y)	-zSIND(Y)
3	zSIND(Y)	-zCOSD(Y)
4	-zSIND(Y)	-zCOSD(Y)
5	-zCOSD(Y)	-zSIND(Y)
6	-zCOSD(Y)	zSIND(Y)
7	-zSIND(Y)	zCOSD(Y)